Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Полученные соотношения нетрудно обобщить на случай, когда имеются различные типы дефектов. Пусть число таких типов дефектов равно n, а дефекты каждого типа образуют Пуассоновский ансамбль. Тогда все дефекты также образуют Пуассоновский поток (1) суммарной интенсивностью, равной сумме интенсивностей:

,

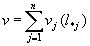где l*j –предельный размер j-го типа дефектов.

С учетом формулы (2) для суммарной вероятности отказов будем иметь: 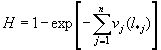, (9)

где интенсивности потоков пропущенных при контроле дефектов находятся по формуле [4]:

.

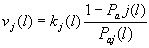
Соответствующие вероятности обнаружения находятся по формуле (6):

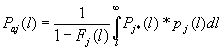, в которую входят функция Fj(l) распределения дефектов j-го типа по размерам и соответствующая плотность вероятности pj(l). Условная вероятность обнаружения P*j(l) оценивается по формуле (7) с пороговым значением l0j и параметром lj для каждого типа дефектов.

Таким образом для оценки вероятности отказов при наличии дефектов различных типов и системе обнаружения дефектов нужно знать следующие вероятностные и числовые характеристики:

Функции распределения дефектов по размерам; Математические ожидания числа обнаруженных дефектов; Пороговые значения обнаружения; Параметры системы обнаружения дефектов; Критические размеры дефектов.

Различные типы предельных состояний характеризуется критическими размерами дефектов, зависящими от свойств материала, от температуры, от условий нагружения и других факторов. Если какие-либо параметры являются случайными, то полученные вероятности имеют смысл условных вероятностей. Основным источником неопределенности является предельное значение размеров дефектов. Этот параметр зависит от ряда случайных факторов. Условные вероятности отказов будут функциями этих параметров. Для вычисления безусловных вероятностей отказов используется формула полной вероятности:

.

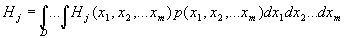Здесь p(x1,x2,…xm) – совместная плотность вероятности параметров. Интегрирование проводится по всей области D изменения параметров.

Вероятность отказов H0 к моменту очередного контроля t=t0 определяется вероятностью необнаружения дефектов размером l, превышающим критический размер l*. При продолжении эксплуатации дефекты, размеры которых не превышали предельных значений, подрастают и с течением времени могут достичь критических размеров.

Пусть к моменту времени t=t0 имеется одиночный размером l. Этот дефект системой контроля может быть обнаружен с вероятностью 1-Pa(l). Рост дефектов будем описывать уравнением (2).

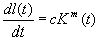(10)

где c и m- эмпирические константы, 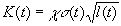- коэффициент интенсивности напряжений, зависящий от уровня напряжений, от размеров дефекта, от свойств материала и других факторов.

Решение уравнения (10), получаемое, как правило, численно с начальным условием l(t0)=l0, зависит от ряда случайных факторов. Эта зависимость определяется случайным характером К, неопределенностью свойств материала и т.д. Обозначим вектор случайных параметров через у с компонентами у1, у2, у3…ур. Тогда решение уравнения (10) можно представить в виде

l(t)= l(y1, y2, y3…yp;t) (11)

К моменту времени t размер дефекта l(t) будет случайным с плотностью вероятности pl(l;t), где t играет роль параметра. Для нахождения распределения pl(l;t) воспользуемся правилами вычисления распределений для детерминистических функций случайных величин (3). В частности, если имеется детерминистическая функция (11), то функция распределения Fl(l;t) находится так:

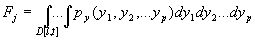(12)

где область интегрирования находится из условия l(t)= l(y1, y2, y3…yp;t)< l.

Остаточный ресурс  определяется как продолжительность эксплуатации после очередного контроля, в течение которого размер дефекта подрастает до критического значения l*. Он находится как корень уравнения

l()=l* (13)

Даже при фиксированных значениях l* ресурс будет случайной величиной. Это связано со случайной зависимостью l(t). Дополнительную неопределенность вносит случайный характер критического размера l*, зависящего от случайных факторов. Плотность вероятности находится по тем же правилам, что и распределение (12).

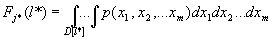(14)

Рекомендуем скачать другие рефераты по теме: дипломы шуточные, реферат принципы.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата