Claw.ru | Рефераты по математике | Овалы Кассини и пузыри в моделировании мягких оболочек Овалы Кассини и пузыри в моделировании мягких оболочек | Категория реферата: Рефераты по математике | Теги реферата: персонал реферат, инновационный менеджмент | Добавил(а) на сайт: Косомов. Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата   -

Примечание: 1. Условие существования деформированных меридианов: (a = R = const, 0 ≤ f ≤ a ).

2. R = a = A1 A2 / 2 = √(f ²+ d² ) = 10 см.

3. h = 2b = K1 K2 = d ²/ f ².

4. h' = 2b' = C1 C2 = 2 √ (d² – f ²).

5. r = B1 B2 / 2 = √ (f ²– d ²).

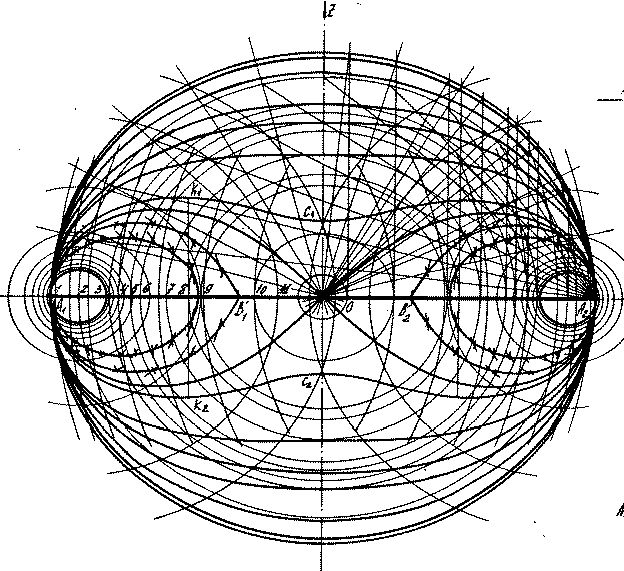
Рис. 27. Схема построения меридиан деформированной сферы

Следует отметить, что построенные по уравнению деформированной сферы (36) меридианы хорошо вписываются в, так называемые, кривые изменения радиуса меридиана, деформированного без изгиба, полученные с помощью дифференциального уравнения, основанного на условиях безызгибности деформации /13/ :

(3 – R2 / R1) х (d R2 / d Θ) – (R2 d / d Θ) х  (R2 / R1) = 0,   (44)

где R1 и  R2                - соответственно меридиональный и окружной радиусы кривизны оболочки вращения;

Θ – угол приложения тангенциальных усилий.       

Кроме того, по данным работы /5/, меридианы оболочек, построенных с помощью эластик Эйлера, практически совпадают с аналогичными меридианами деформированной сферы. При этом одна из кривых Кассини (лемниската) также является циклоидой и имеет тот же порядок функциональной зависимости, что и эластики (Рис.28).

Таким образом, общие закономерности формоизменения  напряженных оболочечных конструкций под нагрузкой с изменением кривизны овалов Кассини позволяют использовать последние для моделирования процессов формоизменения оболочечных конструкций в процессе их деформирования под нагрузкой.

Модифицированное уравнение (36) не зависит от формы деформированной оболочки и выражается соотношением размеров осей симметрии. Следовательно, для расчета предельных состояний оболочек различных форм достаточно, подставляя значения констант, определять геометрические и физические параметры. Установленные физические и геометрические аналогии позволяют использовать их при проектировании оболочечных конструкций для определения напряженности состояния, мест концентрации напряжений, требующих усиления разгружающими элементами, предполагаемых мест разрушения под нагрузкой, а также областей складкообразования.

Эволюция развития формоизменения оболочки под нагрузкой поля напряжения сил давления рабочей среды позволяет вскрыть механизм разрушения оболочек, а также определить запасы прочности и предельные состояния нагруженных оболочечных конструкций.

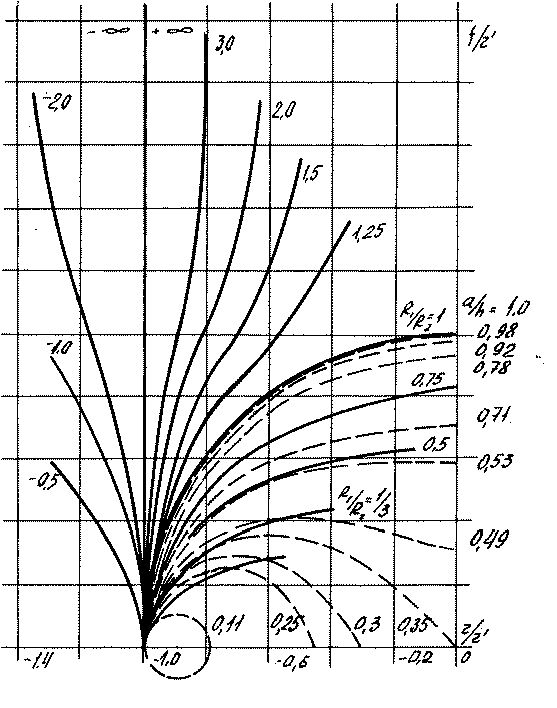
Рис. 28 Графики деформированных меридиан (пунктирная линия) и дифференциальных кривых, построенных с помощью эластик Эйлера.

4. Зависимость натяжения мягкой оболочки от соотношения геометрических размеров.

Рассмотрим зависимость натяжения замыкающей оболочки от уровня напряжения рабочей среды (третье положение).

Например, наложение конфигураций линий уровня пары взаимодействующих частиц (точечных зарядов) представляет суммарную линию, имеющую форму сплюснутого или вытянутого овала с соотношением размеров полуосей симметрии соответственно больше или меньше единицы. Для определения зависимости натяжения деформированной мягкой оболочки от напряжения рабочей среды рассмотрим усилия, при действии которых два мыльных пузыря, прижатые друг к другу, находятся в равновесии.

Если сдвоенные пузыри свободно висят в воздухе, сохраняя сферическую форму, то в этом случае сближение центров сфер, равное (2m), мало по отношению к первоначальному межцентровому расстоянию, равному (2R), площадь контактного пятна эквивалентна радиусу сферы / 2 /.

Определим силу, с которой притягиваются прикоснувшиеся два мыльных пузыря:

F = - DUn / m = 4 p R m T @ 2x2T.                                           (17)

Установлено, что сила притяжения прикоснувшихся пузырей пропорциональна их радиусу и первоначальному межцентровому расстоянию (2R), то есть площади пятна контакта (x2), где (x2 @2R m). Формообразование мягких оболочек с помощью моделей мыльных пузырей показано на рис.20 /19/.   Следует отметить, что при слиянии пузырей образуется мембрана, а слившиеся пузыри теряют сферическую форму и замыкающая оболочка приобретает форму вытянутого овалоида (рис.20,б). Такую форму принимает также цилиндрическая оболочка с соотношением размеров длины к диаметру (1< a/b < SQR(2)).

В соответствии с принятым ранее условием любая полость замкнутой оболочки может быть представлена пузырьковой моделью, то есть блоком соприкасающихся упругих сфер, диаметр которых равен высоте (диаметру) замыкающей оболочки. Для этого впишем пару взаимодействующих упругих сфер в мягкую оболочку с заданным соотношением размеров, затем станем надувать их избыточным давлением газа. Повышение давления в сферах приведет к увеличению межцентрового расстояния, уменьшению диаметра и площади мембраны, перераспределению натяжений пропорционально радиусам кривизны. При увеличении соотношения размеров замыкающей оболочки в пределах (SQR(2) < a/b < 2) произойдет взаимное отталкивание упругих сфер, пропорциональное площади мембраны и уровню давления в них. При этом кривизна замыкающей оболочки между вписанными сферами обратится в нулевую, а в торцах станет равной радиусу вписанных сфер.

Рекомендуем скачать другие рефераты по теме: решебник 10 11, проблема реферат.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата