Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Отметим, что если А¹ 0, то кривая (1) является параболой, если А=0, то прямой.

Лемма 1.2. Площадь s криволинейной трапеции, ограниченной кривой у=Ах2+Вх+С, проходящей через точки М1 (-h; y1), M2 (0, y2), M3 (h, y3) (рис. 2) выражается формулой

(2)

Доказательство. Подставляя в уравнение у=Ах2+Вх+С координаты точек М1, М2, М3, получаем у1=Аh2-Вh+С; у2=С; у3=Аh2+Вh+С, откуда следует, что

2Аh2+2С=у1+у3; С=у2 (3)

Учитывая соотношение (3), имеем

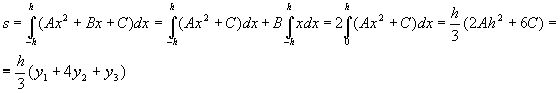
Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой y=f(x). Разобьем отрезок [a, b] на 2p равных отрезков точками a=x0<x1<x2<...<x2k<x2k+1<x2k+2<...<x2n-1<x2n=b, а кривую y=f(x) с помощью прямых x=xk на 2n соответствующих частей точками М0 , М1 , М2 , ..., М2k , М2k+1 , М2k+2, ..., М2n-2 , М2n-1 , М2n (рис. 3).

Через каждую тройку точек

М0 М1 М2 , ..., М2k М2k+1 М2k+2, ..., М2n-2 М2n-1 М2n

проведем кривую вида у=Ах2+Вх+С (см. лемму 1.1). В результате получим n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной трапеции, соответствующей отрезку [x2k, x2k+2], приближенно равна площади соответствующей “параболической” трапеции, то по формуле (2) имеем [в данном случае h=(b-a)/(2n)]

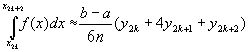
где yk=f(xk), k=0, 1, 2, ...,2n. Складывая почленно эти приближенные равенства, получаем приближенную формулу

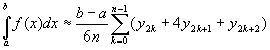
или в развернутом виде

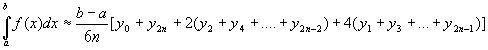
Эта формула называется формулой парабол или формулой Симпсона.

В формуле параболы значение функции f(x) в нечетных точках разбиения х1, х3, ..., х2n-1 имеет коэффициент 4, в четных точках х2, х4, ..., х2n-2 - коэффициент 2 и в двух граничных точках х0=а, х1, х2n =b - коэффициент 1.

Геометрический смысл формулы Симпсона очевиден: площадь криволинейной трапеции под графиком функции f(x) на отрезке [a, b] приближенно заменяется суммой площадей фигур, лежащих под параболами (прямыми).

В полных курсах высшей математики доказывается, что если функция f(x) имеет на [a, b] непрерывную производную четвертого порядка, то абсолютная величина погрешности формулы Симпсона не больше чем

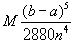
где М - наибольшее значение на отрезке [a, b]. Выше отмечалось, что погрешность формулы трапеций оценивается числом

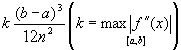
Так как n4 растет быстрее, чем n2, то погрешность формулы Симпсона с ростом n уменьшается значительно быстрее, чем погрешность формулы трапеций. Этим и объясняется, что формула Симпсона позволяет получить большую точность, чем формула трапеций.

Для сравнения точности приближенных формул вычислим еще раз интеграл , но теперь по формуле Симпсона при n=4. Разобьем отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=1/(1+x) в этих точках у0=1,0000, у1=0,8000, у2=0,6667, у3=0,5714, у4=0,5000.

По формуле Симпсона получаем

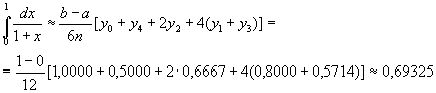
Оценим погрешность полученного результата. Для подынтегральной функции f(x)=1/(1+x) имеем: f(4)(x)=24/(1+x)5 , откуда следует, что на отрезке [0, 1] . Следовательно, можно взять М=24, и погрешность результата не превосходит величины 24/(2880× 44),0б0004. Сравнивая приближенное значение с точным, заключаем, что абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций.

Как отмечалось выше, приближенные формулы для вычисления определенного интеграла применяют в тех случаях, когда первообразная подынтегральной функции не выражается через элементарные функции.

Вычислим, например, интеграл 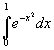по формуле Симпсона с точностью до 0,001.

Чтобы выбрать необходимое для получения заданной точности число 2n, найдем f(4)(x). Последовательно дифференцируя функцию f(x)=, получаем

Рекомендуем скачать другие рефераты по теме: украинские рефераты, реферат финансы.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата