Приближенное вычисление определенных интегралов

| Категория реферата: Рефераты по математике
| Теги реферата: реферат скачать управление, темы рефератов по биологии
| Добавил(а) на сайт: Халски.

f(4)(x)=4(4х4-12х2+3)

Так как на отрезке [0, 1] £ 1, ½4х4-12х2+3½ £5, то . Следовательно, можно взять М=20. Используя формулу оценки погрешности, имеем 20/2880n4<1/1000, откуда n4 >1000/144. Для того чтобы выполнялось это неравенство, достаточно взять n=2, т.е. 2n=4.

Разобьем теперь отрезок [0, 1] на четыре равные части точками х0=0, х1=1/4, х2=1/2, х3=3/4, х4=1 и вычислим приближенно значения функции f(x)=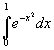в этих точках у0=1,0000, у1=0,9394, у2=0,7788, у3=0,5698, у4=0,3679. Применяя формулу Симпсона, получаем

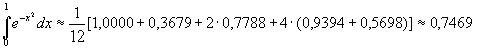
Таким образом, 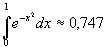с точностью до 0,001. Итак, разбив отрезок [0, 1] всего на четыре равные части и заменив рассматриваемый интеграл суммой, стоящей в правой части формулы Симпсона, мы вычислили данный интеграл с необходимой точностью.

В заключении отметим, что каждый из изложенных методов приближенного вычисления интегралов содержит четкий алгоритм их нахождения, что позволяет широко применять эти методы для вычислений на ЭВМ. Таким образом, указанные методы - эффективное средство вычисления интегралов. Для интегралов, которые нельзя выразить через элементарные функции, с помощью ЭВМ и простейших приближенных методов можно составить таблицы их значений.