Расчет адгезионных характеристик металлов в модели обобщенного потенциала Хейне-Абаренкова

М.В. Мамонова, Р.В. Потерин, В.В. Прудников, Омский государственный университет, кафедра теоретической физики

Явление возникновения связи между поверхностными слоями разнородных конденсированных тел, приведенных в соприкосновение, получило название адгезии. С физической точки зрения, адгезия определяется силами межмолекулярного взаимодействия, наличием ионной, ковалентной, металлической и других типов связи. Возникает необходимость определения характеристик адгезионного взаимодействия различных материалов как с точки зрения прикладной, так и фундаментальной науки о поверхностных явлениях.

В предлагаемой работе в рамках метода функционала плотности проведен расчет адгезионных характеристик для ряда металлов. Исследованы влияния различных приближений, учитывающих дискретность кристаллической структуры и неоднородность электронного газа в межфазной области раздела. Для расчета влияния электрон-ионного взаимодействия на адгезионные характеристики металлов нами был впервые использован обобщенный псевдопотенциал Хейне-Абаренкова. Проведен сравнительный анализ результатов, полученных с его использованием, с результатами, полученными с привлечением иных моделей, в частности, псевдопотенциала Ашкрофта.

Метод функционала плотности состоит в решении вариационной задачи о нахождении минимума энергии системы электронов, рассматриваемой на фоне заданного положительного заряда. В качестве пробных функций электронного распределения, как правило, выбирают решения формально линеаризованного уравнения Томаса-Ферми, а вариационным параметром считают обратную длину экранирования .

Рассмотрим два полуограниченных металла, занимающих области z<-D и z>D. Пусть положительный заряд фона распределен в соответствии с формулой

где и - плотности заряда фона; - ступенчатая функция. Решение линеаризованного уравнения Томаса-Ферми с использованием граничных условий, отражающих непрерывность электростатического потенциала (z) и электрической индукции d/dz при z=D, а также конечность потенциала на бесконечности, позволяет при связи (z)=-4n(z)/ получить следующее выражение для плотности электронного распределения n(z) в системе:

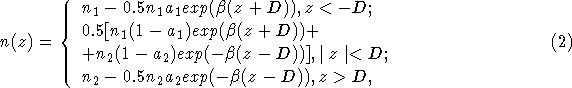
где  

Определим межфазную энергию взаимодействия контактирующих металлов, приходящуюся на единицу площади, как интеграл по z от объемной плотности энергии основного состояния электронного газа:

В рамках модели "желе" объемная плотность энергии неоднородного электронного газа может быть представлена в виде градиентного разложения:

где

есть плотность энергии однородного электронного газа в атомных единицах, включающая последовательно электростатическую, кинетическую, обменную и корреляционную энергии, а

где

- фермиевский волновой вектор,   являются соответственно градиентными поправками второго порядка на неоднородность электронного газа для кинетической энергии в приближении Вейцзекера-Киржница и обменно-корреляционной энергии в приближении Вашишты-Сингви (VS) [1]. Приближение VS является наиболее употребимым для большинства металлов. Учет только поправки для кинетической энергии без рассмотрения влияния соответствует приближению хаотических фаз (ПХФ).

Поправки к межфазной энергии, связанные с учетом дискретности распределения положительного заряда, вычисляются в рамках модели псевдопотенциала Хейне-Абаренкова:

усредненного по кристаллическим плоскостям, параллельным поверхности металлов, и будут характеризоваться параметрами и межплоскостными расстояниями . В результате поправка, связанная с электрон-ионным взаимодействием, принимает вид:

Рекомендуем скачать другие рефераты по теме: курсовая работа по экономике, сочинения по литературе.





1  2  3  4 | Следующая страница реферата