Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Метод конечных элементов

Выберем произвольный треугольник (с номером e). Обозначим его вершины  и . Каждому узлу треугольника поставим в соответствие функцию формы

,        (5)

где ,  A – площадь треугольника. Тогда температуру в пределах треугольника можно определить с помощью функций форм и значений температуры  в узловых точках

.      (6)

Функционал (4) можно представить в виде суммы функционалов , каждый из которых отражает вклад в функционал (4) элемента с номером e

.         (7)

Минимум функционала (4) находим из условия

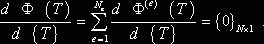      (8)

Функционал  можно представить в виде

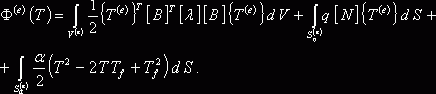  (9)

Здесь , глобальный вектор  температур 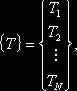  ,  - матрица градиентов, которая для функций формы (5) примет вид 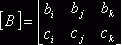, . Локальный вектор температур 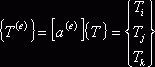. Здесь матрица геометрических связей  имеет размерность . Элементы этой матрицы определяются следующим образом: ; все остальные элементы равны нулю.

Продифференцируем функционал (9):

Из выражения (8) с учетом последнего соотношения получаем , где матрица теплопроводности элемента ; вектор нагрузки элемента  .

В силу особенностей проведенной триангуляции можно выделить три группы конечных элементов. В первую входят треугольники, у которых сторона i – j принадлежит одной из внешних границ. Во вторую – те, у которых та же сторона принадлежит одной из внутренних границ. И, наконец, третью группу составляют элементы, стороны которых лежат внутри рассматриваемой области.

В зависимости от того, к какой группе принадлежит конечный элемент с номером e, матрица  и вектор  будут определяться несколько различным образом.

Обозначим

.

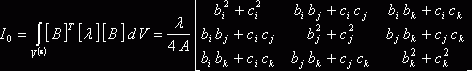Поверхностные интегралы можно посчитать с помощью относительных координат . Отрезки, соединяющие любую фиксированную точку P треугольника e c его вершинами, разбивают этот элемент на три треугольные части площадью . Координаты  определяются из соотношений .

Используя относительные координаты, можно получить следующие соотношения:

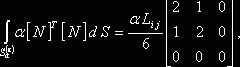
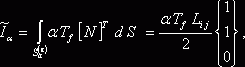
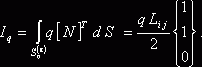
Если конечный элемент с номером e принадлежит к первой группе, то . Если ко второй, то . Наконец, если элемент принадлежит к третьей группе, то .

Вектор температур, удовлетворяющий условию (8) минимума функционала (4), находим решением системы линейных алгебраических уравнений

Рекомендуем скачать другие рефераты по теме: оформление доклада титульный лист, социальные реферат.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата