|
(3) |
где q — любое целое число, а m ≥ 0.
Смысл чисел m и q станет более наглядным, если представлять себе векторы вида (3) при m=0 как точки с целыми координатами параболы k(x, y) = 0, лежащей в плоскости (x, y). (Вы понимаете, почему это парабола?) Тогда полученные нами целочисленные решения неравенства k(x, y) ≥ 0. показывают, что все точки с целыми координатами, лежащие на параболе k(x, y) = 0 и внутри неё, получаются сдвигами целых точек этой параболы на векторы (m, m) (рис. 3). Удобно считать, что число m (m=0, 1, 2, ...) — номер параболы, на которой лежит точка (x, y), a q = x–y = 0, ±1, ±2, ... — номер точки на этой параболе.
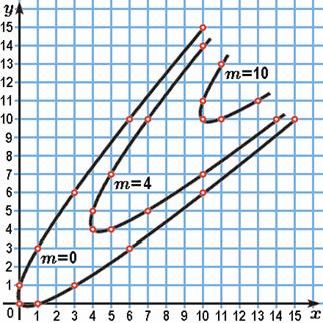
Рис. 3.
Поскольку условия задачи симметричны относительно перестановки координат векторов, достаточно доказать все утверждения для таких векторов (x, y), что x ≥ y, т.е. для векторов вида (3) с q ≥ 0.
Докажем достаточность условия в пункте а) задачи. По формуле суммы арифметической прогрессии
|
1 + 2 + ... + (q–1) + m + q = m + |
q(q + 1) 2 |
; |
|
0 + 1 + ... + (q–2) + m + (q–1) = m + |
q(q – 1) 2 |
. |
Поэтому формулы
(x, y) = (1, 0) + (2, 1) + ... + (q–1, q–2) + (m+q, m+q–1) при q>0
| Разрешается частичное копирование контента в виде анонса при условии размещения прямой ссылки на источник. | © 2006-2024 «Claw.RU» © 2006-2024 «Рефератики.РФ» |
Главная