РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЯТИТОЧЕЧНЫМ МЕТОДОМ АДАМСА – БАШФОРТА

Работу выполнил студент гр.И-29 Уханов Е.В.

Кафедра “Системы и Процессы Управления”

“ХАРЬКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ”

Харьков 2001

ВВЕДЕНИЕ

Во многих областях науки и техники , а также отраслях наукоемкой промышленности , таких как : авиационная , космическая , химическая , энергетическая  , - являются весьма распространенные задачи прогноза  протекания процессов ,  с дальнейшей их коррекцией .

Решение такого рода задач связано с необходимостью использования численных методов , таких как : метод прогноза и коррекции , метод Адамса-Башфорта , метод Эйлера , метод Рунге-Кута , и др.  При этом , стоит задача решения системы линейных дифференциальных уравнений первого порядка одним из методов интегрирования , на произвольном промежутке времени . Одним из оптимальных методов дающих высокую точность результатов – является пяти точечный метод прогноза и коррекции Адамса-Башфорта . Для повышения точности метода используется трех точечный метод прогноза и коррекции с автоматическим выбором шага , что приводит к универсальному методу интегрирования систем дифференциальных уравнений произвольного вида на любом промежутке интегрирования  .

Разработка программных средств реализующих расчет точного  прогноза протекания процессов , является важнейшей вспомогательной научно-технической задачей .

Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта .

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка :

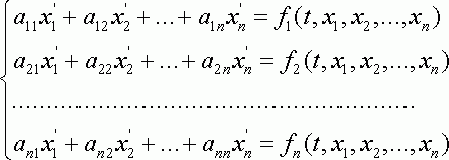                          (1.1)

тогда как :

               А = 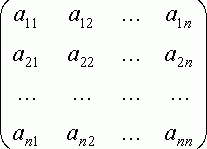                                                         (1.2)

 где  А заданная матрица размером  N x N .

  - вектор с N координатами , который подлежит определению ;

N – произвольное целое число ;

заданные вектора правых частей с N  координатами .

    С  использованием метода прогноза и коррекции Адамса-Башфорта пятого порядка  , необходимо получить значения  неизвестных для заданных  временных интервалов . Для  стартования  метода необходимо использовать метод прогноза и коррекции   третьего порядка с переменным шагом  , на заданных временных промежутках ..

2. МЕТОДЫ РЕШЕНИЯ

2.1. Метод прогноза и коррекции

Метод прогноза и коррекции относится к задачам класса Коши , а именно к численным решениям многошаговыми методами .

Рассмотрим задачу Коши :

            ,                                                   (2.1.1)

Подставим в (2.1.1) точное решение  y(x)  , и проинтегрируем это уравнение на отрезке   , тогда получим :

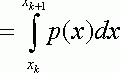
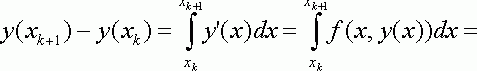                  (2.1.2)

      где в последнем член предполагаем , что   p(x)   полином , аппроксимирующий   f(x,y(x))  . Чтобы построить этот полином , предположим , что    - приближения к решению в точках              . Будем считать для начала , что узлы Xi  расположены равномерно с шагом  h . тогда  fi  = f(xi,yi), ( i=k,k-1,k-2,…,k-N) есть приближения к   f (x,y(x))  в точках   и мы в качестве P  возьмем интерполяционный полином для выбора данных (xi,fi) ,

( i =k,k-1,k-2,…,k-N) . Таким образом , P – полином степени N , удовлетворяющий условиям  P(xi)=fi  , ( i = k,k-1,k-2,…,k-N) .  В принципе , можем проинтегрировать этот полином явно , что ведет к следующему методу  :

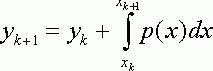                                                                           (2.1.3)

         В простейшем случае , когда  N=0  , полином  P  есть константа  , равная fk  ,  и (2.1.3) превращается в обычный метод Эйлера :

                                                                                       (2.1.4)

         Если  N=1 , то P есть линейная функция , проходящая через точки 

Рекомендуем скачать другие рефераты по теме: сестринские рефераты, конспект урока культура.





1  2  3  4 | Следующая страница реферата