Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

(xk-1,fk-1)  и (xk,fk) , т.е. 

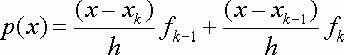                                              (2.1.5)

     интегрируя этот полином  от Xk  до Xk+1  , получим следующий метод :

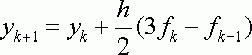                                                                  (2.1.6)

         который является двухшаговым , поскольку использует информацию в двух точках  xk  и   xk-1  . Аналогично , если N=2  , то P  - есть кубический интерполяционный полином , а соответствующий метод определяется формулой  :

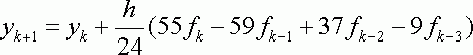                   (2.1.7)

                Отметим , что метод (2.1.6) – есть метод Адамса-Башфорта второго порядка , (2.1.7) – метод Адамса-Башфорта четвертого порядка  .

            Для стартования метода  (2.1.7)  необходимы сведения о четырех предыдущих точках . Соответственно данный метод требует вычисления стартующих данных . Воспользуемся для нахождения второй точки одношаговым методом Эйлера , который имеет вид :

                                    

             Таким образом , подставляя начальные условия, мы находим вторую точку . Следует заметить , что степень точности совпадает со степенью точности остальных методов , что является существенным фактором в стартовании метода прогноза и коррекции .

                Ввиду того , что стартовые методы имеют более низкий порядок , в начале приходится считать с меньшим шагом и с использованием большего промежутка времени . В данном случае метод Эйлера для дальнейшего интегрирования не оправдывает себя . Для этих целей воспользуемся трехшаговым методом прогноза и коррекции с переменным шагом .

          Рассуждая также , как для метода Адамса-Башфорта , который излагается в работах : [1],[2],[3]  ,  мы мы приходим к формулам :

Прогноз :

                                                                       (2.1.8)

Коррекция :

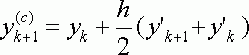                                                        (2.1.9)

где  h  - шаг интегрирования , изменяющийся на малом промежутке времени  в соответствии с условиями Рунге :

                     ,

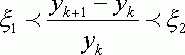где в свою очередь  - малое конкретное значение , при невыполнении условия которого увеличивается шаг  h=h*N  а - малое конкретное значение , при невыполнении условия шаг соответственно уменьшается  h=h/N , где N  - некоторое целое число больше единицы .

Оптимально , для вычисления новой точки , с помощью метода прогноза и коррекции  , используется формула :

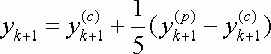                                                  (2.1.10)

Таким образом, мы воспользовались простым трех шаговым методом прогноза и коррекции  , для стартования метода Адамса-Башфорта . Преимущества данного  метода заключаются :в его высокой точности , авто подборе шага , что во много раз повышает точность самого метода Адамса-Башфорта , и делает его оптимальным для задач такого рода .

Метод Адамса-Башфорта использует уже посчитанные значения в точке Xk  и в предыдущих точках . В принципе , при построении интерполяционного полинома , мы можем использовать и точки Xk+1,Xk+2,… . Простейший случай при этом состаит в использовании точек Xk+1,Xk,…,Xk-N

 и построения интерполяционного полинома степени  N+1  , удовлетворяющего условиям  P(Xi)=fi , (I=k+1,k,…,k-N) .  При этом возникает класс методов , известных как методы Адамса-Моултона . Если  N=0  , то  p – линейная функция , проходящая через точки  (Xk,fk) и  (Xk+1,f k+1) , и соответствующий метод :

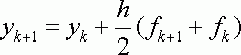                                                                   (2.1.11)

Рекомендуем скачать другие рефераты по теме: сестринские рефераты, конспект урока культура.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата