Симметрии многогранника системы независимости

О.В. Червяков, Омский государственный университет, кафедра математического моделирования

1.  Введение

Пусть E = { e1,e2,,en} - некоторое множество мощности n. Системой независимости на множестве E называется непустое семейство J его подмножеств, удовлетворяющее условию: если Jи I, то I.

Множества семейства называется независимыми множествами. Максимальные по включению множества из называются базисами.

Автоморфизмом системы независимости называется такое взаимооднозначное отображение  множества E на себя, что (I)(e)для любого независимого множества I. Группу автоморфизмов системы независимости будем обозначать через Aut().

Пусть RE - евклидово пространство, ассоциированное с E посредством взаимоодназначного соответствия между множеством координатных осей пространства RE и множеством E. Иными словами, RE можно понимать как совокупность вектор-столбцов размерности n с вещественными компонентами, индексированными элементами множества E. Всякому S E сопоставим его вектор инциденций по правилу: xSe= 1 при eS , xSe= 0 при eS. Очевидно, что это правило задает взаимооднозначное соответствие между 2E и вершинами единичного куба в RE. Многогранник системы независимости определим как P() = Conv(xI | I). Ясно, что векторы инциденций независимых множеств системы независимости , и только они, являются вершинами многогранника P() [4].

Пусть PRE - произвольный многогранник. Симметрией многогранника P назовем такое невырожденное аффинное преобразование  пространства RE, что (P)(x)=P. Как известно, всякое невырожденное аффинное преобразование  определяется невырожденной (nn)-матрицей A и сдвигом hRE, то есть (x)=Ax+h при xRE [1]. Очевидно, что невырожденное аффинное преобразование  пространства RE является симметрией многогранника P() тогда и только тогда, когда для любого I существует такое J, что (xI) = xJ.

Симметрию с нулевым сдвигом будем называть линейной симметрией. Очевидно, что множество всех симметрий многогранника P является группой относительно суперпозиции отображений, а множество линейных симметрий - ее подгруппой. Группу симметрий многогранника P мы будем обозначать через S(), а ее подгруппу линейных симметрий - через L().

Ранее в [3] была доказана изоморфность групп L() и Aut() для матроида , в [2] - изоморфность группы линейных симметрий многогранника паросочетаний и группы автоморфизмов соответствующего графа. Пользуясь аналогичными методами, легко доказать изоморфность групп L() и Aut() для произвольной системы независимости .

В настоящей работе показано, что группа симметрий многогранника системы независимости выписывается с помощью подгруппы L() и семейства некоторых специальных преобразований пространства RE.

Рассмотрим задачу комбинаторной оптимизации на системе независимости с аддитивной целевой функцией:

(1)

где ve0 - вес элемента eE. Пусть имеется симметрия многогранника P со сдвигом xH. Тогда задача (1) сводится к задаче, размерность которой не больше, чем E-H.

Ниже приведены понятия и факты, необходимые для дальнейшего изложения.

Пусть H. H-отображением будем называть линейное невырожденное преобразование  пространства RE, удовлетворяющее условию: для любого I существует такое J, что (xI) = xJH, где под JH подразумевается симметрическая разность множеств J и H.

Без ограничения общности будем считать, что размерность многогранника P равна n, ибо в противном случае существует элемент eЕ, не содержащийся ни в каком независимом множестве и, следовательно, вместо E можно рассматривать множество E{e} .

2.  Структура группы симметрий системы независимости

Итак, будем считать, что у нас зафиксирована система независимости на множестве E={e1,e2,,en}; RE-пространство, ассоциированное с E; P-многогранник системы независимости .

Так как , то для всякой симметрии  со сдвигом h найдется такое H, что h=xH. Таким образом, группу S() можно разбить на непересекающиеся классы , где SH - класс симметрий многогранника P(), имеющих сдвиг xH. Это позволяет свести описание группы S() к описанию.

Лемма 1. Пусть SH, a 1 - аффинное невырожденное преобразование пространства RE. Тогда 1SH, если и только если существует такое 2L(), что 1 = jj2.

Доказательство. Так как L() и SH являются подмножествами группы S(), то j1 = jj2S(). Очевидно, что j1 имеет сдвиг xH. Обратно, если j1  SH, то j2 = j-1j1S(), причем с нулевым сдвигом. Следовательно, j2L().

Таким образом, наличие какой-либо (любой) симметрии из SH позволяет с помощью группы L() найти весь класс SH.

Лемма 2. Пусть j - невырожденное преобразование пространства RE. Преобразование jSH тогда и только тогда, когда j=j1j2, где

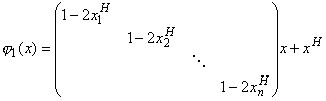
a j2 - H-отображение.

Доказательство. Прямыми вычислениями легко убедиться, что j1(xS) = xSH для любого SE, и j1-1=j1.

Рекомендуем скачать другие рефераты по теме: реферат экологические проблемы, современные рефераты.





1  2  3 | Следующая страница реферата