
Симметрии многогранника системы независимости
| Категория реферата: Рефераты по математике
| Теги реферата: понятие курсовой работы, продажа рефератов
| Добавил(а) на сайт: Potjomkin.
Предыдущая страница реферата | 1 2 3 | Следующая страница реферата
Если
2 - H-отображение, то для любого I![]() существует
такой J
существует
такой J![]() , что 2(xI) = xJH. То есть 12(xI) = x(JH)H
= xJ.
, что 2(xI) = xJH. То есть 12(xI) = x(JH)H
= xJ.
Следовательно, = 12 - симметрия многогранника P и jSH.
Если
же jSH, то для любого I![]() существует
такой J
существует
такой J![]() , что (xI)=xJ.
Следовательно, 2(xI) =1-1(xI) = 1-1(xJ)
= 1(xJ) = xJH
, что (xI)=xJ.
Следовательно, 2(xI) =1-1(xI) = 1-1(xJ)
= 1(xJ) = xJH
Значит, 2 - H-отображение. Данная лемма дает возможность свести поиск
представителя класса SH к поиску одного H-отображения. Причем, если
H-отображений для данного H![]() не
существует, то SH=.
не
существует, то SH=.
Поиск H-отображения существенно упрощается с помощью следующего предложения.
Предложение 1. Матрица H-отображения булева.
Доказательство.
Так как {ej}![]() для любого j{1n}, то ,по определению H-отображения, вектор (x{ej}), являющийся j-м
столбцом матрицы отображения, булев, что и требовалось доказать.
для любого j{1n}, то ,по определению H-отображения, вектор (x{ej}), являющийся j-м
столбцом матрицы отображения, булев, что и требовалось доказать.
3. Понижение размерности задачи на системе независимости
Рассмотрим оптимизационную задачу (1) и перейдем к полиэдральной постановки этой задачи
|
|
(2) |
где v - это вектор, компоненты которого - веса соответствующих элементов. Очевидно, что решение задачи (2), при условии "поиска по вершинам", будет являться вектором инциденций решения задачи (1). Кроме того, если существует симметрия многогранника P с матрицей A и сдвигом h, и x* решение задачи
|
|
(3) |
то вектор x = Ax*+h - решение задачи (2).
Предложение 2. Пусть (x) = Ax+xH - симметрия многогранника P и v - произвольный вектор с положительными компонентами. Тогда вектор vTA имеет по крайней мере H неположительных компонент.
Доказательство.
По лемме 2, симметрия представима в виде суперпозиции отображений 1, описанного в лемме 2, и H-отображения 2. Матрица A является
произведением матриц преобразований 1 и 2. Так как H![]() H
H![]() H , то
существует такое множество I
H , то
существует такое множество I![]() , что 2
(xI) = xH. Причем, так как любое подмножество H принадлежит
, что 2
(xI) = xH. Причем, так как любое подмножество H принадлежит ![]() H, то
в силу линейности 2, IH.
Следовательно, матрица преобразования 2 принимает вид
H, то
в силу линейности 2, IH.
Следовательно, матрица преобразования 2 принимает вид
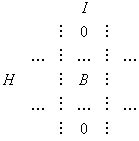
Здесь I и H - столбцы и строки, соответствующие элементам из этих множеств, а блок B - некоторая булевa матрица. При умножении матрицы преобразования 2 на матрицу преобразования 1 блок B заменяется на блок (-B). Затем, при умножении вектора vT на матрицу A, получается вектор, у которого компоненты, соответствующие элементам множества I, неположительные. Очевидно, что элементы, имеющие неположительные веса, не принадлежат оптимальному множеству задачи (3). Следовательно, исключая из рассмотрения эти элементы, переходим к задаче
|
|
(4) |
где v* = vTA, D-совокупность элементов, у которых соответствующие компоненты вектора v* неположительные. Вектор инциденций решения этой задачи есть оптимальный вектор задачи (3). Причем, по предыдущему предложению, размерность задачи (4) не больше, чем E-H.
Пример
1. Пусть E = {1,2,3,4}, ![]() - система
независимости, базисы которого являются множества {1,2,3} и {3,4}. Пусть
H={1,3}. Тогда матрица H-отображения принимает вид
- система
независимости, базисы которого являются множества {1,2,3} и {3,4}. Пусть
H={1,3}. Тогда матрица H-отображения принимает вид
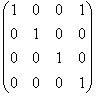
a
симметрия многогранника системы независимости ![]() -
-
Рекомендуем скачать другие рефераты по теме: реферат экологические проблемы, современные рефераты.
Категории:
Предыдущая страница реферата | 1 2 3 | Следующая страница реферата
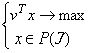
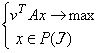
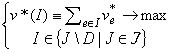
 Главная
Главная