Важность трехдиагональной формы обусловлена тем, что некоторые методы преобразований подобия позволяют привести произвольную матрицу к этому частному виду.
3. Матрица A называется ортогональной, если
АТА = Е,
где Ат—транспонированная матрица A, а Е—единичная матрица. Очевидно, матрица, обратная ортогональной, эквивалентна транспонированной.
4. Матрицы А и В называются подобными, если существует такая несингулярная матрица Р, что справедливо соотношение
В = Р-1АР.
Основные свойства собственных значений.
1. Все п собственных значений симметричной матрицы размерности пХп, состоящей из действительных чисел, действительные. Это полезно помнить, так как матрицы, встречающиеся в инженерных расчетах, часто бывают симметричными.
2. Если собственные значения матрицы различны, то ее собственные векторы ортогональны. Совокупность п линейно независимых собственных векторов образует базис рассматриваемого пространства. Следовательно, для совокупности линейно независимых собственных векторов
Xi, где i == 1,. . ., n,
любой произвольный вектор в том же пространстве можно выразить через собственные векторы. Таким образом,
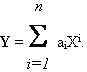
3. Если две матрицы подобны, то их собственные значения совпадают.
Из подобия матриц A и В следует, что
В = Р-1АР.
Так как АХ = l Х,
то Р-1АХ = l Р-1Х.
Если принять Х == РY, то Р-1АРY = l
Y, а ВY == l Y.
Таким образом, матрицы A и В не только имеют одинаковые собственные значения, но и их собственные векторы связаны соотношением
Х = Р Y.
4. Умножив собственный вектор матрицы на скаляр, получим собственный вектор той же матрицы. Обычно все собственные векторы нормируют, разделив каждый элемент собственного вектора либо на его наибольший элемент, либо на сумму квадратов всех других элементов.
3.ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ.
Пожалуй, наиболее очевидным способом решения задачи на собственные значения является их определение из системы уравнений
(A - l
E) Х == 0,
которая имеет ненулевое решение лишь в случае, если det(A - l
E)=0. Раскрыв определитель, получим многочлен п-й степени относительно l
, корни которого и будут собственными значениями матрицы. Для определения корней можно воспользоваться любым из методов, описанных в гл. 2. К сожалению, в задачах на собственные значения часто встречаются кратные корни. Так как итерационные методы, в этих случаях не гарантируют получение решения, то для определения собственных значений следует пользоваться другими итерационными методами.
Определение наибольшего собственного значения методом итераций
Рекомендуем скачать другие рефераты по теме: доклади по биологии, рефераты по политологии.
Предыдущая страница реферата |
1
2
3
4
5
6
7
8
9
10
11 |
Следующая страница реферата
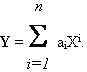
 Главная
Главная