Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

имеет вид:

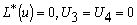(20)

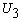где и 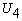связаны с компонентами 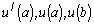вектора соотношением (14). Краевая задача (19) называется самосопряженной тогда и только тогда, когда 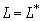и каждая из двух компонент 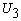и 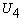является линейной комбинацие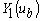й и 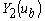, т.е. 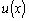пропорциональна .

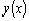Один из определителей:

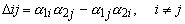
матриц-блоков

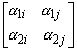
должен быть отличным от нуля. Чтобы иметь возможность сравнить эти результаты с теми. которые были получены в предыдущем параграфе, предположим. что 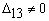. Далее, выберем такие 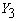и 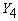, чтобы строки матрицы А были линейно независимы.

Например, положим 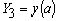и .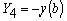

При этом матрица А примет вид:

(21).

Из формулы (19) следует, что .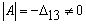

Тогда

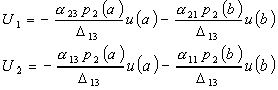(22)

Подставляя матрицы (20) и (9) в соотношение (14) имеем (14а):

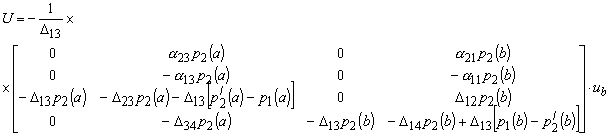
Следовательно, граничные условия сопряженной задачи имеют вид:

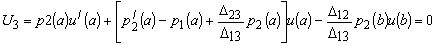(22)

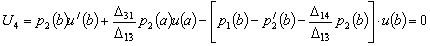(23)

Для того, чтобы краевые задачи были самосопряженными необходимо, чтобы 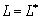и чтобы каждая из компонент 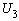и 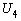являлась линейной комбинацие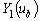й и 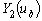. Как указывалось выше, 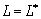тогда и только тогда, когда 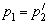. При этом условия (21) и (20) принимают вид:

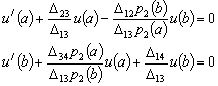(24)

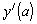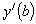Разрешая равенства относительно и при 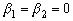и заменяя 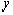на 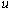, получаем:

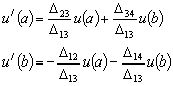(25)

Сравнивая граничные условия (24) и (25), заключаем, что они совпадают тогда и только тогда, когда:

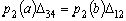(26)

Рекомендуем скачать другие рефераты по теме: бесплатные рефераты на тему, сочинение евгений онегин.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата