Предыдущая страница реферата | 1  2  3 | Следующая страница реферата

Пусть рекурсивно над '. Тогда X и [] определяются рекурсивными дизъюнкциями бескванторных формул и вида (1).

Случай 1. Одна из есть конечная конъюнкция неравенств вида . Такой будут удовлетворять все элементы поля , за исключением конечного числа алгебраических элементов, т.е. X есть множество требуемого вида.

Случай 2. Все содержат хотя бы одно равенство вида t(x) = 0. Тогда множество X не содержит ни одного трансцендентного элемента, следовательно, существует , которой удовлетворяют трансцендентные элементы, но тогда содержит только одни неравенства . Таким образом, мы приходим к случаю 1 с заменой X на его дополнение.

Лемма 5. Если функция вычислима в системе , то для любых принадлежит подсистеме системы , порожденной элементами .

Доказательство. См. в [1].

Теорема 6. Пусть , рекурсивные множества. Тогда каждое поле содержит одно из полей .

Доказательство. Пусть . Тогда найдется вычислимая функция f(x), что . По лемме 5, f(ai), есть значение некоторого терма сигнатуры т.е. рациональной функции с коэффициентами из поля . Значит, , т.е. .

Обратно, пусть , , т.е. ti(ai) = bi для некоторого набора рациональных функций . Тогда посредством вычислимой функции

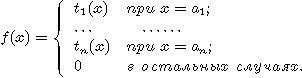
Непосредственно из определения следует, что для любого конечного Y.

Следствие 7. Справедливы следующие утверждения:

1) если X конечное рекурсивное множество и , то любое конечное рекурсивное Y сводится к X;

2) для рекурсивного X имеем: и ;

3) среди рекурсивных m-степеней существует наибольшая, это степень множества X из п.2.

Доказательство. 1. Следует из теоремы.

2. По лемме 4 можно считать, что множество X конечно, а конечно. Тогда существует a . Если и f сводящая функция, то , но по лемме 5 f(a) есть значение некоторой рациональной функции с коэффициентами из , т.е. . Обратно, если существует , то X и [] сводятся друг к другу посредством функции

3. Пусть X конечное рекурсивное множество и . Пусть Y произвольное рекурсивное. Если Y конечно, то по п.1. Если Y коконечно, то по лемме 3, но . Таким образом, упорядочение рекурсивных m-степеней в поле имеет вид:

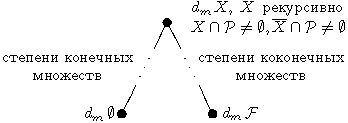
Если в поле достаточно много алгебраических элементов, например, если алгебраически замкнуто, то существует бесконечное число рекурсивных m-степеней.

Следствие 8. Пусть поле алгебраически замкнутое характеристики 0, a рекурсивная m-степень, и не является наибольшей среди рекурсивных. Тогда:

1) существует счетное число рекурсивных степеней, несравнимых с a;

2) существует счетное число попарно несравнимых степеней , таких, что ;

3) существует счетное число попарно несравнимых степеней , таких, что ;

4) порядок на рекурсивных m-степенях плотный.

Рекомендуем скачать другие рефераты по теме: конспект лекций, доклад по биологии.





Предыдущая страница реферата | 1  2  3 | Следующая страница реферата