Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Доведення теореми для 2х2 матриць.

Нехай .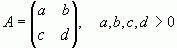

Тоді .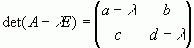

Напишемо характеристичне рівняння для матриці А:

.

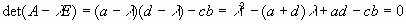Це квадратне рівніння з дискримінантом:

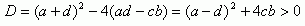
І тому

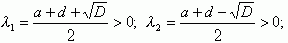
Тобто твердження теореми 1 і 2 доведені, якщо r=l 1.

Знайдемо власний вектор 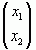, що відповідає власному значенню l 1 з рівності

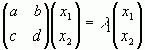
Тоді

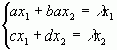, або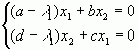

Враховуючи, що

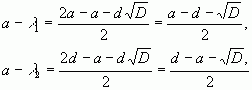
перепишемо систему у вигляді:

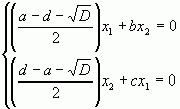
Але 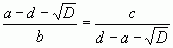і тому рівняння системи пропорціональні, а це означає, що одне з них можна відкинути.

Знайдемо x1 з першого рівняння системи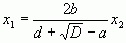

Щоб довести, що власний вектор можна вибрати додатним, достатньо перевірити, що 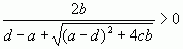,тому що поклавши отримаємо x1>0.

Враховуючи, що b>0 треба довести, що ,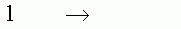

але це випливає з того, що 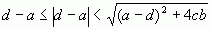, бо cb>0.

Таким чином третє твердження доведено, а з ним доведена теорема.

Визначення: Матриця А n-го порядку зветься нерозкладною, якщо однаковим переставленням рядків та стовпців її не можна привести до виду 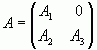, де А1, А2 - квадратні матриці розмірів k x k та (n-k) x (n-k) відповідно. Для 2х2 матриць 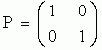це означає, що 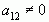та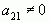

Рекомендуем скачать другие рефераты по теме: профессиональные рефераты, бесплатные доклады.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата