Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Очевидно, що рівняння системи пропорційні, тому одне з них можна відкинути. Знайдемо y1 з першого рівняння: 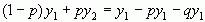або 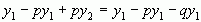звідки 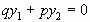, але 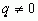, бо в протилежному випадку дана матриця мала б вигяд: 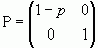, а тоді матриця 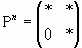мала б нульовий елемент 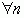, що суперечить умові. Тому можна записати, що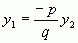

Доведемо тепер твердження 1 теореми.

Розглянемо матрицю S, стовпцями якої є власні вектори матриці P. Нам необхідно отримати зручну формулу для Pn.

Позначимо .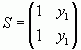

Оскілки 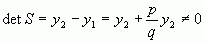, то існує S-1. Перепишемо рівняння 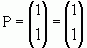та 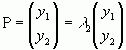у матричній формі

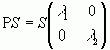або .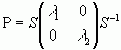

Відкіля 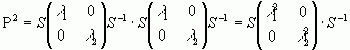і взагалі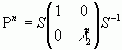

Знайдемо границю Pn:

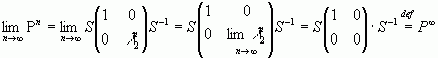
Твердження 1 теореми доведено.

Доведемо тепер, що рядки матриці 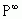однакові. Для цього обчиcлимо .

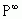Оскільки 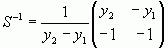, то 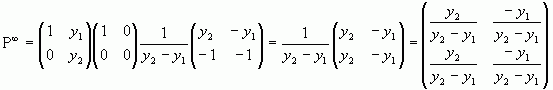Ми бачимо, що рядки матриці 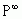- однакові. Доведемо тепер, що їх елементи додатні. Для цього врахуємо отриману раніше залежність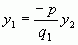

Для того, щоб довести треба довести, що 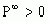, треба довести, що 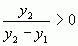та .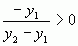

Маємо

,

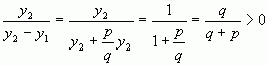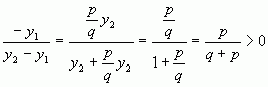, тому що p>0 і q >0

Теорема доказана.

Зауваження1 В процесі доведення ми вивели, що для 2х2 матриць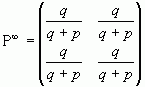

Зауваження2 Позначимо 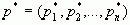рядки граничної матриці 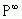. Тоді 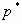можна знайти з умови:

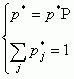
Доведення.

Оскільки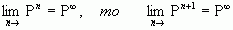

Зівдки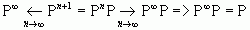

Або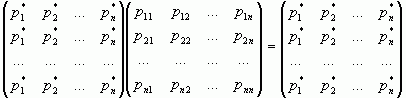

Рекомендуем скачать другие рефераты по теме: профессиональные рефераты, бесплатные доклады.

Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата