Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

аij     (i = )

т.е. определяется минимальный выигрыш для игрока 1 при условии, что он примет свою i-ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i = iо, при которой этот минимальный выигрыш будет максимальным, т.е. находится

аij = =                     (1).

Определение. Число , определённое по формуле (1) называется нижней чистой ценой игры и показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2.

Игрок 2 при оптимальном своём поведении должен стремится по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскивается

аij

т.е. определяется max выигрыш игрока 1, при условии, что игрок 2 применит свою j-ю чистую стратегию, затем игрок 2 отыскивает такую свою j = j1 стратегию, при которой игрок 1 получит min выигрыш, т.е. находит

aij = =                       (2).

Определение. Число , определяемое по формуле (2), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счёт своих стратегий может себе гарантировать игрок 1.

Другими словами, применяя свои чистые стратегии игрок 1 может обеспечить себе выигрыш не меньше , а игрок 2 за счёт применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем .

Определение. Если в игре с матрицей А =, то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры

u = =.

Седловая точка – это пара чистых стратегий (iо,jо) соответственно игроков 1 и 2, при которых достигается равенство  = . В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Математически это можно записать и иначе:

                  

где i, j – любые чистые стратегии соответственно игроков 1 и 2; (iо,jо) стратегии, образующие седловую точку.

Таким образом, исходя из (3), седловой элемент  является минимальным в iо-й строке и максимальным в jо-м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (iо,jо) игроков 1 и 2, образующая седловую точку и седловой элемент , называется решением игры. При этом iо и jо называются оптимальными чистыми стратегиями соответственно игроков 1 и 2.

Пример 1

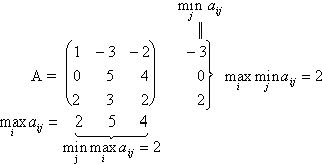
Седловой точкой является пара (iо = 3; jо = 1), при которой u == = 2.

Заметим, что хотя выигрыш в ситуации (3;3) также равен 2 ==, она не является седловой точкой, т.к. этот выигрыш не является максимальным среди выигрышей третьего столбца.

Пример 2

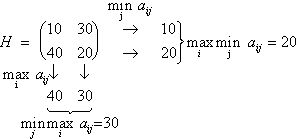
Из анализа матрицы выигрышей видно, что , т.е. данная матрица не имеет седловой точки. Если игрок 1 выбирает свою чистую максиминную стратегию i = 2, то игрок 2, выбрав свою минимаксную j = 2, проиграет только 20. В этом случае игроку 1 выгодно выбрать стратегию i = 1, т.е. отклониться от своей чистой максиминной стратегии и выиграть 30. Тогда игроку 2 будет выгодно выбрать стратегию j = 1, т.е. отклониться от своей чистой минимаксной стратегии и проиграть 10. В свою очередь игрок 1 должен выбрать свою 2-ю стратегию, чтобы выиграть 40, а игрок 2 ответит выбором 2-й стратегии и т.д.

Смешанное расширение матричной игры.

Исследование в матричных играх начинается с нахождения её седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой седловой точки заканчивается исследование игры. Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путём применения чистых стратегий случайно, с определённой вероятностью.

Рекомендуем скачать другие рефераты по теме: рефераты бесплатно, конспект по математике.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата