Предыдущая страница реферата | 15  16  17  18  19  20  21  22  23  24  25 | Следующая страница реферата

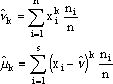
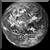
Дисперсией случайной величины X, называется центральный момент второго порядка случайной величины X.

Дисперсия является мерой концентрации результатов конкретных испытаний над случайной величиной X.

Свойства.

1. Чем меньше дисперсия, тем более тесно группируются результаты конкретных испытаний относительно математического ожидания.

Пусть дисперсия мала, тогда мало каждое слагаемое суммы (xi-n)2pi. Тогда для , xi которое по модулю резко отличается от математического ожидания n, pi - мало. Следовательно, большую вероятность наступления могут иметь лишь те xi, которые по модулю мало отличаются от математического ожидания.

2. Если дисперсия равна 0, то X - const.

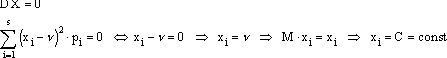
3.

D(X+C)=DX

Y=X+C

Y’=Y-MY=X+C-M(X+C)=X+C-MX-C=X-MX=X’

DY=M(Y’)2=M(X’)2=DX

4.

DCX=C2DX

Y=CX

DY= M(Y’)2=M(Y’)2

Y’=Y-MY=CX-MCX=CX-MCX=C(X-MX)=CX’

DY= M(Y’)2=M(CX’)2=C2M(X’)2=C2DX

5.

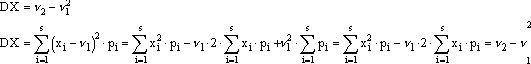
Построим функцию распределения для дискретной случайной величины. Для удобства договоримся, что случайные величины располагаются в порядке возрастания.

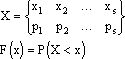
т.е. по определению для любого действительного X, F(x) численно равно вероятности наступления следующего события: в результате испытаний над X оно приняло значение строго меньше x.

Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.

Предыдущая страница реферата | 15  16  17  18  19  20  21  22  23  24  25 | Следующая страница реферата