Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата



Следовательно, на основании III аксиомы теории вероятности результат равняется:

  (сложение вероятностей)

Случайная величина

Пусть имеется вероятностное пространство вида .

Случайной величиной называется измеримая числовая скалярная функция , элементами которой являются элементарные события.

Числовая скалярная функция - это функция, удовлетворяющая следующему условию:

 событие - алгебре и, следовательно, имеет вероятность наступления.

Если произведено испытание, в результате которого произошло некоторое элементарное событие . В соответствии с функцией  этому элементарному событию соответствует число, которое называется реализацией случайной величины x в данном испытании.

В соответствии с определением случайной величины вводится числовая скалярная функция F(x), , определенная для каждого действительного x и по определению равная вероятности наступления события:

Эта функция называется функцией распределения случайной величины .

Рассмотрим три события:

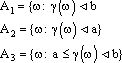
где a<b, a, b - действительные числа.

Свойства:

Покажем, что из факта

A2 Ì s-алгебре

A1 Ì s-алгебре

и равенства  следует, что A3 Ì s.

По определению s-алгебры A3 измерима, поэтому можно принять III аксиому теории вероятности:

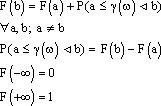
    F(x) - неубывающая функция

Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.

Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата