|
II
|
|
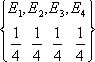
|
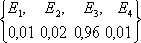
|
Очевидно, что
неопределенность испытания до испытания в первом вероятностном пространстве
выше, чем во втором. Действительно, до испытания в I нельзя ни одному из
событий отдать предпочтения, а во II событие E3 происходит чаще.
Энтропия - мера
неопределенности исхода испытания (до испытания).
Первым, кто
функционально задал выражение для энтропии был Шеннон.
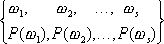 ,
, 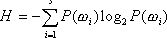
Для
вероятностного пространства:
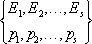
Энтропия
задается выражением: 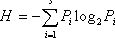 . Если P1=0, то Pi×logPi=0.
. Если P1=0, то Pi×logPi=0.
Самим показать, что:
Если вероятностное пространство не имеет
определенности, т.е. какое-то из Pi=1, а остальные равны 0, то энтропия
равна нулю.
Если элементарный исход равновероятен, т.е. 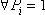 , то энтропия принимает максимальное значение.
, то энтропия принимает максимальное значение.
0£Pi£1, 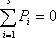
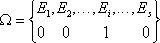
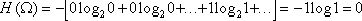 ,
, 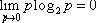
т.о.
вероятности p1, p2, ..., ps обращаются в ноль, например pi, которая равна 1. Но log1=0. Остальные числа также
обращаются в 0, т.к. 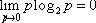 .
.
Докажем, что
энтропия системы с конечным числом состояний достигае максимума, когда все
состояния равновероятны. Для этого рассмотрим энтропию системы как функцию
вероятностей p1, p2, ..., ps и найдем условный
экстремум этой функции, при условии, что 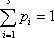 .
.
Пользуясь
методом неопределенных множителей Лагранжа, будем искать экстремум функции: 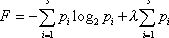 .
.
Дифференцируя
по p1, p2, ..., ps и приравнивая производные
нулю получим систему:
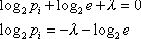 i=1, ..., s
i=1, ..., s
Откуда видно, что экстремум достигается при равных между собой p1.
Т.к.
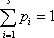 , то p1=
p2=, ..., = ps= 1/s.
, то p1=
p2=, ..., = ps= 1/s.
Еденицей
измерения энтропии является энтропия вероятностного пространства вида: 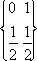
Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.
Предыдущая страница реферата |
8
9
10
11
12
13
14
15
16
17
18 |
Следующая страница реферата
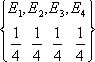
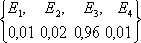
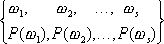 ,
, 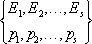
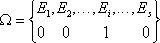
 Главная
Главная