Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата



A1  -алгебре

и равенства следует, что A3  .

По определению -алгебры A3 измерима, поэтому можно принять III аксиому теории вероятности:

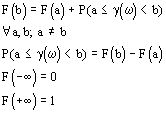
F(x) - неубывающая функция

Если x<y, то

т.к. , то преобразования верны.

Для всех технических приложений функцию распределения можно считать направленной слева.

В силу того, что функция распределения не убывает, она однозначно задает стчетно-аддитивную меру на поле, порожденном всеми полуинтервалами ненулевой длины.

По введенному полю построим борелевскую алгебру. Обозначим ее . Возьмем произвольное число B не принадлежащее полю. Это точка или сегмент. Т.к. множество получено с помощью счетной суммы или счетного пересечения множеств принадлежащих -алгебре, то и это множество принадлежит -алгебре и, следовательно, существует вероятность наступления события B. Следовательно, имеет место следующее эквивалентное определение измеримой функции.

Функция называется измеримой, если для любого BО множество

алгебре

где

множество, полученное следующим образом:

Функция g(x) называется борелевской функцией, если для любого B множество

Борелевская функция - функция, определяемая на системе борелевских множеств.

В функциональном анализе показано, что все известные аналитические функции являются борелевскими.

ТЕОРЕМА:

Пусть g(x) борелевская функция, - случайная величина, т.е. измеримая функция. Тогда функция

является измеримой и, следовательно, случайной величиной.

Рекомендуем скачать другие рефераты по теме: изложение по русскому 6 класс, реферат анализ.

Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата