Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

3. Основное состояние триона

Ввиду полного отсутствия каких-либо малых параметров, при нахождении энергии основного состояния триона, как и в случае иона Н", обычно используют вариационные методы.

Как уже упоминалось, основная задача в любом вариационном методе заключается в выборе вариационной функции. С одной стороны - она должна быть как можно более простой, так как, для того, чтобы получить минимальное, относительно всех варьируемых параметров, значение энергии, требуется вычислить это значение для большого количества наборов значений этих параметров, что иногда требует серьезных вычислительных усилий. Желательно, чтобы максимальную часть этих вычислений можно было бы проделать аналитически. С другой стороны - пробная волновая функция должна максимально соответствовать по форме точной волновой функции системы, иначе полученное значение энергии будет сильно отличаться от истинного.

Есть два возможных пути построения нужной вариационной функции. Первый - это искать ее в виде суммы большого числа простых для аналитики функций, а в качестве вариационных параметров использовать главным образом весовые коэффициенты перед этими слагаемыми. Этот метод очень хорош, когда требуется получить энергию состояния с высокой точностью, и поэтому заранее предполагается использование большого количества варьируемых параметров. С различными вариациями этот метод применялся для расчетов трионов и других трехчастичных систем неоднократно [7-9]. Энергия трионов в некоторых расчетах получалась с точностью до 16 знаков, а количество подгоночных параметров достигало 1000.

Другой путь построения хорошей вариационной функции необходим, если нам не нужно получить результаты с очень высокой точностью, но было бы желательно иметь под рукой не очень сложную аналитическую функцию, удобную для использования в каких-либо оценках и расчетах. Для сравнения - представьте насколько проще пользоваться функцией

f(x)=ехр(-3x+1),

чем численным рядом

f(x)≈2.718 - 8.155x+12.232x2+...,

до тех пор пока не угадать, что второе есть всего лишь разложение первого в степенной ряд.

Для построения такой вариационной функции необходимо правильно учесть все эффекты, которые вносят основной вклад в энергию системы. В том, как и в какой форме их учесть, есть определенный элемент творческого "угадывания". Как правило, функции, построенные таким образом, труднее интегрировать, чем набор простых функций, который использовался в первом подходе, поэтому использовать их для высокоточных вычислений путем увеличения подгоночных параметров обычно нецелесообразно. Зато даже при использовании небольшого количества параметров они дают значение энергии системы с хорошей точностью. Пойдем по второму пути и посмотрим, как построить хорошую функцию с небольшим, числом подгоночных параметров, которая позволила бы получить энергию основного состояния триона при любом значении отношения масс электрона и дырки. Необычность задачи состоит в том, что одна и та же функция при различных значениях вариационных параметров должна с хорошей точностью описывать не только Х+ и X" трионы, но и предельные случаи - ион водорода Н" и молекулу водорода Н2+, различие между волновыми || функциями которых очень велико. В качестве основы для нашей функции возьмем двумерный аналог пробной функции, предложенной в 1944 году Чандрасекаром [10] для трехмерного иона водорода H-:

ψ(r1,r2)=[ехр(-ar1-br2)+ехр(-br1-ar2)](1+cR), (1)

Она состоит из симметризованного произведения двух водородоподобных функций с различными радиусами орбит электронов и поляризационного множителя. Величины r1 и r2r1-r2|. Вариационные параметры а и b имеют смысл обратных радиусов орбит двух электронов, а параметр c обеспечивает рост волновой функции при увеличении расстояния между электронами, то есть учитывает поляризационные эффекты.

Функция (1) учитывает, пусть и в простом виде, все эффекты, которые вносят основной вклад в энергию иона. А именно:

1. Кулоновское взаимодействие каждого из электронов с ядром.

Функция (1) содержит в основе водородоподобные функции (exp(-ar)).

2. Экранирование дальнего электрона ближним.

В слагаемое ехр(-ar1-br2) волновые функции электронов (ехр(-ar1,ехр(-br2)) входят с разными показателями экспонент, что соответствует различным радиусам орбит электронов.

3. Обменное взаимодействие.

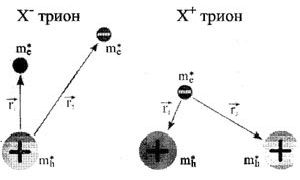
Рис 1. X- и X+ трионы, общий вид

Волновая функция симметризована и не меняется при замене r1↔r2, то есть допускает обмен электронов.

4. Поляризация.

Как уже упоминалось, она учтена наличием множителя (1+сR).

Так как эти вклады присутствуют и являются основными как для трехмерного иона H-, так и для его двумерного аналога, то неудивительно, что с помощью функции (1) получается хорошее приближение энергии связи иона. В обоих случаях ошибка в определении энергии составляет менее 10% от ее значения (за нуль энергии принято состояние атом водорода + свободный электрон).

Посмотрим, что изменится, если мы применим волновую функцию (1) к трионам с различными значениями отношения масс. Заметим, что волновая функция триона должна содержать в своей основе функцию основного состояния экситона (электрон + дырка), которая совпадает по форме ехр(-аr) с функцией атома водорода. Причем, энергия триона (в особенности - X- триона) должна определяться вкладами тех же, как и в ионе H-, эффектов: поляризации, экранирования и обменного взаимодействия. Поэтому есть основания предполагать, что с помощью функции (1) можно с неплохой точностью (не худшей, чем для иона водорода) получить энергию любого X- триона.

Проблема возникает при моделировании X+ трионов по мере приближения к противоположному от H- пределу - молекуле H2+, в связи с наличием у них двух тяжелых частиц. В этом пределе движение этих частиц "замораживается", и они перестают вносить вклад в кинетическую энергию комплекса. Это приводит к известному факту, что энергия связи молекулы H2+ почти в 4 раза превышает энергию связи иона H-. При увеличении отношения масс электрона и дырки вблизи предела H2+, кинетическая энергия колебаний двух тяжелых частиц, возрастающая пропорционально корню из этого отношения масс, очень быстро начинает вносить существенный вклад в энергию, триона. Уже при отношении масс σ=0.1 энергия связи этого комплекса уменьшается почти вдвое по сравнению с пределом H2+ (σ→0). Поэтому для правильного вычисления энергии X+ триона, особенно при малых отношениях масс, необходимо в дополнение к вышеперечисленным эффектам учесть возможность продольных колебаний одинаковых частиц возле некоторого равновесного расстояния. Так как других эффектов, которые могут внести большой вклад в энергию триона при каком-либо отношении масс больше не видно, то пробная функция, в которой все эти эффекты будут учтены, должна с хорошей точностью давать энергию комплекса при любом отношении масс.

Пример такой функции приведён в работе [11]:

Рекомендуем скачать другие рефераты по теме: характеристика реферата, реферат перспектива.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата