
Тройные и кратные интегралы
| Категория реферата: Рефераты по математике
| Теги реферата: изложение, решебник по русскому
| Добавил(а) на сайт: Igoshin.
Предыдущая страница реферата | 2 3 4 5 6 7 8 9 10 11 12 | Следующая страница реферата
2. Цилиндрические координаты.
Отнесём область ![]() к системе цилиндрических координат
к системе цилиндрических координат ![]() , в которой положение точки M в пространстве определяется полярными координатами
, в которой положение точки M в пространстве определяется полярными координатами ![]() ее проекции Р на плоскость Oxy и ее аппликатой (z). Выбирая взаимное расположение осей координат, как указано на рис. 5, установим связь, между декартовыми и цилиндрическими координатами точки М, именно:
ее проекции Р на плоскость Oxy и ее аппликатой (z). Выбирая взаимное расположение осей координат, как указано на рис. 5, установим связь, между декартовыми и цилиндрическими координатами точки М, именно:
![]() (*)
(*)
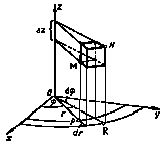
Рис.5
Разобьем область ![]() на частичные области
на частичные области ![]() тремя системами координатных поверхностей:
тремя системами координатных поверхностей: ![]() которыми будут соответственно круговые цилиндрические поверхности, осью которых является ось Оz, полуплоскости, проходящие через ось Оz, и плоскости, параллельные плоскости Оху. Частичными областями
которыми будут соответственно круговые цилиндрические поверхности, осью которых является ось Оz, полуплоскости, проходящие через ось Оz, и плоскости, параллельные плоскости Оху. Частичными областями ![]() служат прямые цилиндры MN (рис. 5). Так как объем цилиндра MN равен площади основания, умноженной на высоту, то для элемента объема получаем выражение
служат прямые цилиндры MN (рис. 5). Так как объем цилиндра MN равен площади основания, умноженной на высоту, то для элемента объема получаем выражение
![]()
Преобразование тройного интеграла ![]() к цилиндрическим координатам производится совершенно аналогично преобразованию двойного интеграла к полярным. Для этого нужно в выражении подынтегральной функции
к цилиндрическим координатам производится совершенно аналогично преобразованию двойного интеграла к полярным. Для этого нужно в выражении подынтегральной функции ![]() переменные x, y, z заменить по формулам (*) и взять элемент объёма равным
переменные x, y, z заменить по формулам (*) и взять элемент объёма равным ![]()
Получим
![]()
Если, в частности, ![]() то интеграл выражает объём V области
то интеграл выражает объём V области ![]()
![]()
Вычисление тройного интеграла в цилиндрических координатах приводится к интегрированиям по r, по ![]() и по z на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра
и по z на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра ![]() то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:
то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:
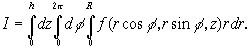
3. Сферические координаты.
Отнесём теперь область интегрирования ![]() к системе сферических координат
к системе сферических координат ![]() . В этой системе координат положение точки M в пространстве определяется её расстоянием r от начала координат (длина радиуса-вектора точки), углом
. В этой системе координат положение точки M в пространстве определяется её расстоянием r от начала координат (длина радиуса-вектора точки), углом ![]() между радиусом-вектором точки и осью Oz и углом
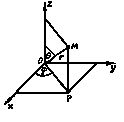
между радиусом-вектором точки и осью Oz и углом ![]() между проекцией радиуса вектора точки на плоскость Oxy и осью Ox (рис. 6). При этом
между проекцией радиуса вектора точки на плоскость Oxy и осью Ox (рис. 6). При этом ![]() может изменятся то 0 до
может изменятся то 0 до![]() а
а ![]() - от 0 до
- от 0 до ![]() .
.
Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.
Категории:
Предыдущая страница реферата | 2 3 4 5 6 7 8 9 10 11 12 | Следующая страница реферата
 Главная
Главная