Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

 

 

 

 

Рис.6

Связь между сферическими и декартовыми координатами легко устанавливается. Из рис.6 имеем

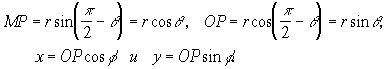
Отсюда

(**)

Разобьем область на частичные области , тремя системами координатных поверхностей: которыми будут

 

 

 

 

 

 

 

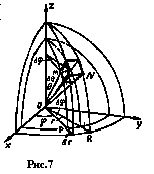
соответственно сферы с центром в начале координат, полуплоскости, проходящие, через ось Оz, и конусы с вершиной в начале координат и с осями, совпадающими с одной из полуосей Оz. Частичными областями служат “шестигранники” (рис. 7). Отбросив бесконечно малые высших порядков, будем рассматривать шестигранник MN как прямоугольный параллелепипед с измерениями, равными: по направлению полярного радиуса, по направлению меридиана, по направлению параллели. Для элемента объема мы получим тогда выражение

Заменив в тройном интеграле по формулам (**) и взяв элемент объема равным полученному выражению, будем иметь

Особенно удобно применение сферических координат в случае, когда область интегрирование - шар с центром в начале координат или шаровое кольцо. Например, в последнем случае, если радиус внутреннего шара , а внешнего , пределы интегрирования следует расставить так:

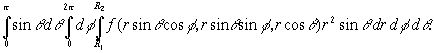
Если - шар, то нужно положить

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата