
Уравнения Курамото-Цузуки
| Категория реферата: Рефераты по математике
| Теги реферата: характер реферат, сочинение 6 класс
| Добавил(а) на сайт: Sukin.
1 2 3 4 | Следующая страница реферата
Уравнения Курамото-Цузуки
Дубровский А.Д., Заверняева Е.В.
Введение
На текущий момент разработано ряд математических моделей вида реакции-диффузии:
|
|
(1) |
в областях:
Химии
Пример. Автокаталитическая реакция.
|
Для этой реакции соответствует задача:
|
Экологии
Теории морфогенеза
Физики плазмы
Теории горения
Другие
Требуется:
классифицировать качественное поведение решения уравнений (1) в зависимости от различных правых частей
классифицировать системы вида (1)
В работе 1975 года Курамото и Цудзуки сделали вывод, что у большинства диссипативных систем существует аналог термодинамической ветви. При всех значениях параметра, исследуемые уравнения имеют однородное по пространству стационарное решение. Это решение устойчиво при λ<λ0. Поведение решений после потери устойчивости термодинамической ветви (λ>λ0) определяется спектром линеаризованной задачи для уравнения (1) в окрестности точки бифуркации λ0. Уравнение, предложенное Курамото и Цудзуки, описывает поведение в окрестностиλ0, вида:
|
|
(2) |
Функция W(R, T) - характеристика отклонения решений системы (1) от пространственно-однородного решения. Таким образом, уравнение (2) описывает только случаи, когда при λ>λ0 решение остается в малой окрестности термодинамической ветви.
Без ограничения общности, в уравнении (2) можно положить с0=0, в этом можно убедится сделав замену переменных W=W´exp(i c0 t). И так получается, вторая краевая задача при условии, что потоки на границе равны нулю:
|
Рекомендуем скачать другие рефераты по теме: контрольная работа 2, виды шпор. Категории:1 2 3 4 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
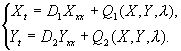
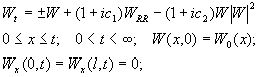
 Главная
Главная