Вычисление координат центра тяжести плоской фигуры I.Координаты центра тяжести.

Пусть на плоскости Oxy дана система материальных точек

P1(x1,y1); P2(x2,y2); ... , Pn(xn,yn)

c массами m1,m2,m3, . . . , mn.

Произведения ximi и yimi называются статическими моментами массы mi относительно осей Oy и Ox.

Обозначим через xc и yc координаты центра тяжести данной системы. Тогда координаты центра тяжести описанной материальной системы определяются формулами:

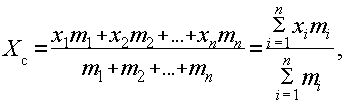
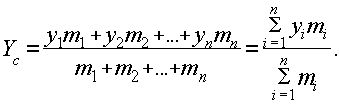
Эти формулы используются при отыскании центров тяжести различных фигур и тел.

1.Центр тяжести плоской фигуры.

Пусть данная фигура, ограниченная линиями y=f1(x), y=f2(x), x=a, x=b, представляет собой материальную плоскую фигуру. Поверхностною плотность, то есть массу единицы площади поверхности, будем считать постоянной и равной d для всех частей фигуры.

Разобьем данную фигуру прямыми x=a, x=x1, . . . , x=xn=b на полоски ширины D x1, D x2, . . ., D xn. Масса каждой полоски будет равна произведению ее площади на плотность d . Если каждую полоску заменить прямоугольником (рис.1) с основанием D xi и высотой f2(x )-f1(x ), где x 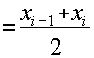, то масса полоски будет приближенно равна

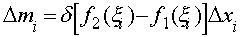(i = 1, 2, ... ,n).

Приближенно центр тяжести этой полоски будет находиться в центре соответствующего прямоугольника:

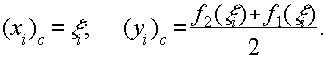
Заменяя теперь каждую полоску материальной точкой, масса которой равна массе соответствующей полоски и сосредоточена в центре тяжести этой полоски, найдем приближенное значение центра тяжести всей фигуры:

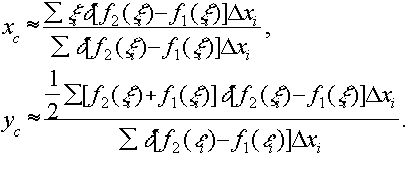
Переходя к пределу при 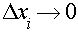, получим точные координаты центра тяжести данной фигуры:

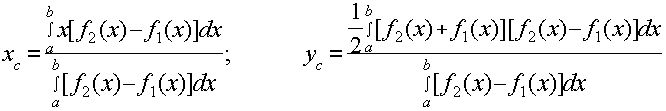
Эти формулы справедливы для любой однородной (т.е. имеющей постоянную плотность во всех точках) плоской фигуры. Как видно, координаты центра тяжести не зависят от плотности d фигуры (в процессе вычисления d сократилось).

2. Координаты центра тяжести плоской фигуры

В предыдущей главе указывалось, что координаты центра тяжести системы материальных точек P1, P2, . . ., Pn c массами m1, m2, . . ., mn определяются по формулам

.

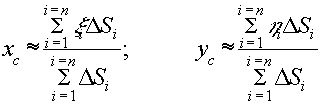В пределе при 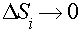интегральные суммы, стоящие в числителях и знаменателях дробей, перейдут в двойные интегралы, таким образом получаются точные формулы для вычисления координат центра тяжести плоской фигуры:

(*)

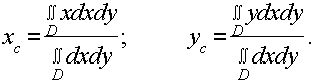Эти формулы, выведенные для плоской фигуры с поверхностной плотностью 1, остаются в силе и для фигуры, имеющей любую другую, постоянную во всех точках плотность g .

Если же поверхностная плотность переменна:

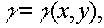
то соответствующие формулы будут иметь вид

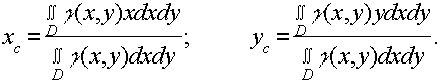
Выражения

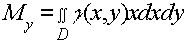
и

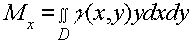
называются статическими моментами плоской фигуры D относительно осей Oy и Ox.

Интеграл 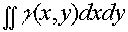выражает величину массы рассматриваемой фигуры.

3.Теоремы Гульдена.

Теорема 1.

Площадь поверхности, полученной при вращении дуги плоской кривой вокруг оси, лежащей в плоскости этой кривой и не пересекающей ее, равна длине дуги кривой, умноженной на длину окружности, описанной центром тяжести дуги.

Теорема 2.

Объем тела, полученного при вращении плоской фигуры вокруг оси, не пересекающей ее и расположенной в плоскости фигуры, равен произведению площади этой фигуры на длину окружности, описанной центром тяжести фигуры.

Рекомендуем скачать другие рефераты по теме: стандарты реферата, океан реферат.





1  2 | Следующая страница реферата