Предыдущая страница реферата | 1  2



II.Примеры.

1)Условие: Найти координаты центра тяжести полуокружности X2+Y2=a2, расположенной над осью Ox.

Решение: Определим абсциссу центра тяжести:

,

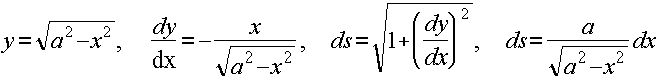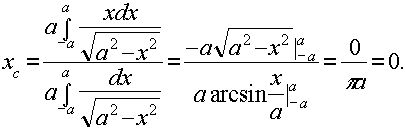
Найдем теперь ординату центра тяжести:

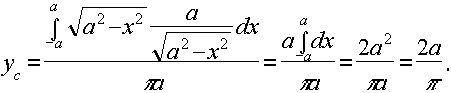
2)Условие: Определить координаты центра тяжести сегмента параболы y2=ax, отсекаемого прямой, х=а (рис. 2)

Решение: В данном случае 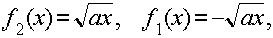поэтому

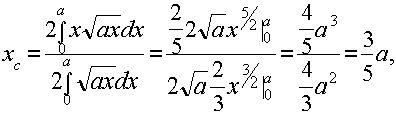
(так как сегмент симметричен относительно оси Ox)

3)Условие: Определить координаты центра тяжести четверти эллипса (рис. 3)

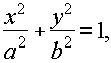
полагая, что поверхностная плотность во всех точках равна 1.

Решение: По формулам (*) получаем:

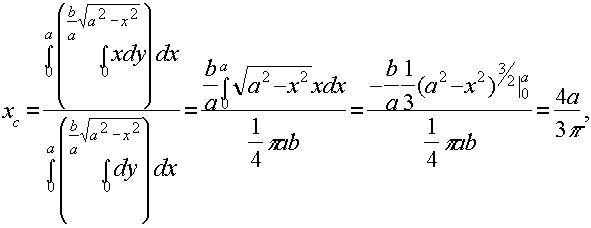
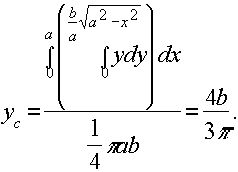
4)Условие:

Найти координаты центра тяжести дуги цепной линии .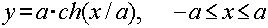

Решение:

1Так как кривая симметрична относительно оси Oy, то ее центр тяжести лежит на оси Oy, т.е. Xc= 0. Остается найти . Имеем 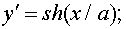тогда

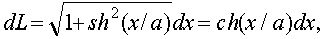
длина дуги

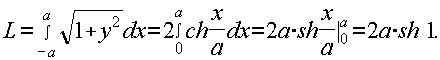
Следовательно,

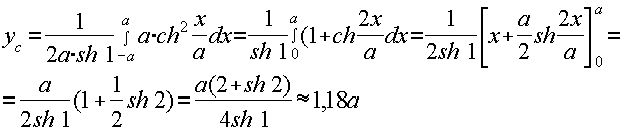
5)Условие:

Пользуясь теоремой Гульдена найти координаты центра тяжести четверти круга

.

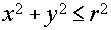Решение:

При вращении четверти круга вокруг оси Ох получим полушар, объем которого равен

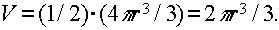
Согласно второй теореме Гульдена,

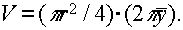
Отсюда

Центр тяжести четверти круга лежит на оси симметрии, т.е. на биссектрисе I координатного угла, а потому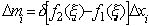

III.СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Данко П.Е., Попов А.Г., Кожевникова Т.Я. “Высшая математика в упражнениях и задачах”, часть 2, “Высшая школа”, Москва, 1999. Пискунов Н.С. “Дифференциальное и интегральное исчисления для втузов”, том 2, “Наука”, Москва, 1965
Скачали данный реферат: Amelfa, Jarkov, Ostapjuk, Ponikarov, Mariam, Зиновий.
Последние просмотренные рефераты на тему: рефераты по биологии, диплом анализ, содержание реферата курсовые работы, контрольная работа 10.





Предыдущая страница реферата | 1  2