
–Ш–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є—П –Ї–≤–∞–љ—В–Њ–≤–Њ–Љ–µ—Е–∞–љ–Є—З–µ—Б–Ї–Є—Е –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–є —Б –њ–Њ–Ј–Є—Ж–Є–є –≤–Њ–ї–љ–Њ–≤–Њ–≥–Њ –Њ–њ–Є—Б–∞–љ–Є—П —Б–Є—Б—В–µ–Љ–љ–Њ—Б—В–Є —Д–Є–Ј–Є—З–µ—Б–Ї–Є—Е –≤–µ–ї–Є—З–Є–љ
| –Ъ–∞—В–µ–≥–Њ—А–Є—П —А–µ—Д–µ—А–∞—В–∞: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –љ–∞—Г–Ї–µ –Є —В–µ—Е–љ–Є–Ї–µ
| –Ґ–µ–≥–Є —А–µ—Д–µ—А–∞—В–∞: —Б–Њ—З–Є–љ–µ–љ–Є–µ –њ–Њ –Ї–∞—А—В–Є–љ–µ, –±—Г–Љ–∞–≥–∞ —А–µ—Д–µ—А–∞—В
| –Ф–Њ–±–∞–≤–Є–ї(–∞) –љ–∞ —Б–∞–є—В: –Р–ї–µ–Ї—Б–∞–љ–і—А–Є–љ–∞.
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3 4 5 6 7 8 9 10 11 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
![]() . (3.2)
. (3.2)
–Ф–ї—П –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є
–њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ—Л —И–Є—А–Є–љ–Њ–є –∞ —Б –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –≤—Л—Б–Њ–Ї–Є–Љ–Є (–љ–µ–њ—А–Њ–љ–Є—Ж–∞–µ–Љ—Л–Љ–Є) —Б—В–µ–љ–Ї–∞–Љ–Є, –њ—А–Є –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–Є –≥—А–∞–љ–Є—З–љ—Л—Е —Г—Б–ї–Њ–≤–Є–є ![]() –Є
–Є ![]() , –њ–Њ–ї—Г—З–∞–µ–Љ –Т =
0. –Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ (3.2) –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П –≤
, –њ–Њ–ї—Г—З–∞–µ–Љ –Т =
0. –Ґ–Њ–≥–і–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ (3.2) –њ—А–µ–Њ–±—А–∞–Ј—Г–µ—В—Б—П –≤
![]() , (3.3)
, (3.3)
–Ї–Њ—В–Њ—А–Њ–µ –і–ї—П –Р ≠ 0 —Д–Њ—А–Љ–∞–ї—М–љ–Њ –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П –њ—А–Є
![]() , n =
0,1,2,3,вА¶ (3.4)
, n =
0,1,2,3,вА¶ (3.4)
–Я–Њ—Б–ї–µ–і–љ–µ–µ —Г—Б–ї–Њ–≤–Є–µ –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –≤–Є–і–µ
![]() , n = 1,2,3,вА¶
(3.5)
, n = 1,2,3,вА¶
(3.5)
–≥–і–µ ![]() - –і–ї–Є–љ–∞ –≤–Њ–ї–љ—Л
–і–µ –С—А–Њ–є–ї—П —Б —З–µ—А—В–Њ–є (
- –і–ї–Є–љ–∞ –≤–Њ–ї–љ—Л
–і–µ –С—А–Њ–є–ї—П —Б —З–µ—А—В–Њ–є (![]() ).
).
–Т—Л—А–∞–ґ–µ–љ–Є–µ (3.5) –Є–Љ–µ–µ—В
—Д–Є–Ј–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї вАУ —Н—В–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ —И–Є—А–Є–љ—Л –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ—Л –Ї –Љ–Њ–і–∞–Љ –і–ї–Є–љ —Б—В–Њ—П—З–Є—Е
–≤–Њ–ї–љ –і–µ –С—А–Њ–є–ї—П, —Б–њ–Њ—Б–Њ–±–љ—Л—Е –Ї —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—О –≤ —Н—В–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ –Є
—Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г—О—Й–Є—Е –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Г, –љ–∞—Е–Њ–і—П—Й—Г—О—Б—П –≤ —П–Љ–µ. –≠—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ
–≤ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ —Б –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –≤—Л—Б–Њ–Ї–Є–Љ–Є —Б—В–µ–љ–Ї–∞–Љ–Є –њ—А–Є—Б—Г—В—Б—В–≤—Г—О—В (–Њ—В–±–Є—А–∞—О—В—Б—П –Є–ї–Є
—А–µ–Ј–Њ–љ–Є—А—Г—О—В) –ї–Є—И—М –Љ–Њ–і—Л –≤–Њ–ї–љ—Л, —Б –і–ї–Є–љ–Њ–є –≤–Њ–ї–љ—Л —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ –і–Њ–ї—М–љ–Њ–є –Њ—Б–љ–Њ–≤–љ–Њ–є –і–ї–Є–љ–µ
–≤–Њ–ї–љ—Л ![]() . –†–µ–∞–ї—М–љ–Њ вАУ
–њ–Њ–ї–Њ–≤–Є–љ–µ —Н—В–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П.
. –†–µ–∞–ї—М–љ–Њ вАУ
–њ–Њ–ї–Њ–≤–Є–љ–µ —Н—В–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П.
–Я–Њ—Б–ї–µ–і–љ–µ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≥–Њ–≤–Њ—А–Є—В –Њ –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–Љ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є–Є –≤ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ –і–ї–Є–љ –≤–Њ–ї–љ –Є–ї–Є –≤–Њ–ї–љ–Њ–≤—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤. –Ъ–≤–∞–љ—В–Њ–≤–∞–љ–Є–µ —Г—А–Њ–≤–љ–µ–є —Н–љ–µ—А–≥–Є–Є –і–ї—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л, –љ–∞—Е–Њ–і—П—Й–µ–є—Б—П –≤ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ, - —Н—В–Њ —Г–ґ–µ —Б–ї–µ–і—Б—В–≤–Є–µ –Њ—В–Љ–µ—З–µ–љ–љ–Њ–≥–Њ –њ–µ—А–≤–Њ–љ–∞—З–∞–ї—М–љ–Њ–≥–Њ –Ї–≤–∞–љ—В–Њ–≤–∞–љ–Є—П –і–µ–±—А–Њ–є–ї–µ–≤—Б–Ї–Є—Е –і–ї–Є–љ –≤–Њ–ї–љ.
–Ч–љ–∞—З–Є—В –ї–Є–љ–µ–є–љ—Л–є –Є–ї–Є —З–∞—Б—В–Њ—В–љ—Л–є —Б–њ–µ–Ї—В—А —Б—В–Њ—П—З–Є—Е –≤–Њ–ї–љ, –Њ–њ–Є—Б—Л–≤–∞—О—Й–Є—Е —Б–Њ—Б—В–Њ—П–љ–Є–µ –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л, –љ–∞—Е–Њ–і—П—Й–µ–є—Б—П –≤ –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ —Б –∞–±—Б–Њ–ї—О—В–љ–Њ –љ–µ–њ—А–Њ–љ–Є—Ж–∞–µ–Љ—Л–Љ–Є —Б—В–µ–љ–Ї–∞–Љ–Є, –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В —Б–Њ–±–Њ–є –Њ—Б–љ–Њ–≤–љ—Г—О –і–ї–Є–љ—Г –≤–Њ–ї–љ—Л (–Њ—Б–љ–Њ–≤–љ—Г—О —З–∞—Б—В–Њ—В—Г) –Є –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –±–Њ–ї—М—И–Њ–є –љ–∞–±–Њ—А –і—А—Г–≥–Є—Е –≤–Њ–ї–љ, —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ –і–Њ–ї—М–љ—Л—Е –њ–Њ–ї–Њ–≤–Є–љ–µ –Њ—Б–љ–Њ–≤–љ–Њ–є. –Х—Б–ї–Є –ґ–µ –±—А–∞—В—М —З–∞—Б—В–Њ—В—Г –≤–Њ–ї–љ –і–µ –С—А–Њ–є–ї—П, —В–Њ —Н—В–Њ –Њ—Б–љ–Њ–≤–љ–∞—П —З–∞—Б—В–Њ—В–∞ –Є –±–µ—Б—З–Є—Б–ї–µ–љ–љ–Њ–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –і—А—Г–≥–Є—Е —З–∞—Б—В–Њ—В, —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–љ–Њ –Ї—А–∞—В–љ—Л—Е –Њ—Б–љ–Њ–≤–љ–Њ–є —З–∞—Б—В–Њ—В–µ.
–Ш–Ј–≤–µ—Б—В–љ–Њ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ, –Њ–њ—А–µ–і–µ–ї—П—О—Й–µ–µ –і–Є—Б–Ї—А–µ—В–љ—Л–є —Б–њ–µ–Ї—В—А —Г—А–Њ–≤–љ–µ–є —Н–љ–µ—А–≥–Є–Є –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л, –љ–∞—Е–Њ–і—П—Й–µ–є—Б—П –≤ –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ —Б –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –≤—Л—Б–Њ–Ї–Є–Љ–Є —Б—В–µ–љ–Ї–∞–Љ–Є
![]() , n = 1, 2, 3, вА¶ (3.6)
, n = 1, 2, 3, вА¶ (3.6)
–і–ї—П –њ–Њ–љ–Є–Љ–∞–љ–Є—П, –ї—Г—З—И–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞—В—М –Є –њ—А–µ–і—Б—В–∞–≤–ї—П—В—М –≤ –≤–Є–і–µ:
![]() , n = 1, 2, 3, вА¶ (3.7)
, n = 1, 2, 3, вА¶ (3.7)
–Х—Й–µ –±–Њ–ї–µ–µ –њ–Њ–љ—П—В–љ—Л–Љ –±—Г–і–µ—В –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ —Н—В–Њ–≥–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ –≤ –≤–Є–і–µ:
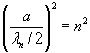 , n = 1, 2, 3, вА¶ , (3.8)
, n = 1, 2, 3, вА¶ , (3.8)
–Њ—В–Ї—Г–і–∞ –≤—Л—В–µ–Ї–∞–µ—В —А–∞–≤–µ–љ—Б—В–≤–Њ
![]() , n = 1, 2, 3, вА¶ , (3.9)
, n = 1, 2, 3, вА¶ , (3.9)
–Я–Њ—Б–ї–µ–і–љ–µ–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В, —З—В–Њ –љ–∞ —И–Є—А–Є–љ–µ –Њ–і–љ–Њ–Љ–µ—А–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ—Л –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ —Г–Ї–ї–∞–і—Л–≤–∞–µ—В—Б—П —Ж–µ–ї–Њ–µ —З–Є—Б—В–Њ –і–µ–±—А–Њ–є–ї–µ–≤—Б–Ї–Є—Е –њ–Њ–ї—Г–≤–Њ–ї–љ (–Є—Е –≥–∞—А–Љ–Њ–љ–Є–Ї), –Ї–∞–ґ–і–∞—П –Є–Ј –Ї–Њ—В–Њ—А—Л—Е –њ–Њ —З–∞—Б—В–Њ—В–µ –≤—Л—И–µ, –∞ –њ–Њ –і–ї–Є–љ–µ –≤–Њ–ї–љ—Л –Љ–µ–љ—М—И–µ –Њ—Б–љ–Њ–≤–љ–Њ–є –Љ–Њ–і—Л –≤ —Ж–µ–ї–Њ–µ —З–Є—Б–ї–Њ —А–∞–Ј. –Т –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ —Б –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –≤—Л—Б–Њ–Ї–Є–Љ–Є —Б—В–µ–љ–Ї–∞–Љ–Є —З–Є—Б–ї–Њ —Н—В–Є—Е –≤–Њ–ї–љ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –±–Њ–ї—М—И–Њ–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ. –Ґ–Њ –µ—Б—В—М, –љ–∞—З–Є–љ–∞—П —Б –≥—А–∞–љ–Є—З–љ–Њ–є —З–∞—Б—В–Њ—В—Л, –Є–Љ–µ–µ—В—Б—П —З–∞—Б—В–Њ—В–љ—Л–є —Б–њ–µ–Ї—В—А –≤–Њ–ї–љ –і–µ –С—А–Њ–є–ї—П. –≠—В–Њ—В —Б–њ–µ–Ї—В—А –ї–Є–љ–µ–є—З–∞—В—Л–є –Є –Њ–љ —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ –≤ —Б—В–Њ—А–Њ–љ—Г —Г–≤–µ–ї–Є—З–µ–љ–Є—П —З–∞—Б—В–Њ—В—Л –і–Њ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–Є.
–Т—Л—И–µ –Љ—Л —А–∞—Б—Б–Љ–Њ—В—А–µ–ї–Є –њ–∞—А–∞–Љ–µ—В—А—Л –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л, –њ–Њ–Љ–µ—Й–µ–љ–љ–Њ–є –≤ –Њ–і–љ–Њ–Љ–µ—А–љ—Г—О –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Г—О —П–Љ—Г —Б –љ–µ–њ—А–Њ–љ–Є—Ж–∞–µ–Љ—Л–Љ–Є —Б—В–µ–љ–Ї–∞–Љ–Є. –Ґ–µ–њ–µ—А—М —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –≤–Њ–ї–љ–Њ–≤—Л–µ –Є –і—А—Г–≥–Є–µ –њ–∞—А–∞–Љ–µ—В—А—Л –і–ї—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж, –љ–∞—Е–Њ–і—П—Й–Є—Е—Б—П –≤ –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —П–Љ–∞—Е, –∞ —В–∞–Ї–ґ–µ –≤ —П–Љ–∞—Е, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ—Л—Е –њ–Њ –≤—Л—Б–Њ—В–µ.
–Э–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–∞—П –≤–Њ–ї–љ–Њ–≤–∞—П —Д—Г–љ–Ї—Ж–Є—П, –њ–Њ–ї—Г—З–∞–µ–Љ–∞—П —А–µ—И–µ–љ–Є–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є—П –®—А–µ–і–Є–љ–≥–µ—А–∞ –і–ї—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л, –љ–∞—Е–Њ–і—П—Й–µ–є—Б—П –≤ –і–≤—Г–Љ–µ—А–љ–Њ–є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–є –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —П–Љ–µ —Б –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ –≤—Л—Б–Њ–Ї–Є–Љ–Є —Б—В–µ–љ–Ї–∞–Љ–Є, –Є–Љ–µ–µ—В –≤–Є–і:
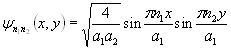 , (3.10)
, (3.10)
0 < x <a1, 0 < y < a2, n1, n2 = 1, 2, 3, вА¶
–≠–љ–µ—А–≥–Є—П –Љ–Є–Ї—А–Њ—З–∞—Б—В–Є—Ж—Л –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П –≤—Л—А–∞–ґ–µ–љ–Є–µ–Љ
–†–µ–Ї–Њ–Љ–µ–љ–і—Г–µ–Љ —Б–Ї–∞—З–∞—В—М –і—А—Г–≥–Є–µ —А–µ—Д–µ—А–∞—В—Л –њ–Њ —В–µ–Љ–µ: –Њ—В—З–µ—В –њ–Њ –њ—А–Њ–Є–Ј–≤–Њ–і—Б—В–≤–µ–љ–љ–Њ–є –њ—А–∞–Ї—В–Є–Ї–µ, —Б–Њ—З–Є–љ–µ–љ–Є—П –њ–Њ –Ї–∞—А—В–Є–љ–∞–Љ.
–Ъ–∞—В–µ–≥–Њ—А–Є–Є:
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3 4 5 6 7 8 9 10 11 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
 –У–ї–∞–≤–љ–∞—П
–У–ї–∞–≤–љ–∞—П