Так как орбиты планет эллиптичны и
постепенно прецессируют, то каждая из них занимает кольцевую область между
двумя круговыми орбитами с радиусами:
|
rπ = (1 –
e)a
|
(1)
|
|
rα = (1 +
e)a
|
(2)
|
где rπ – радиус орбиты в
перигелии,
rα – радиус орбиты в
афелии,
a – большая полуось орбиты.
Этим круговым орбитам соответствуют свои
периоды, а интервал периодов может быть найден по следующей формуле:
|
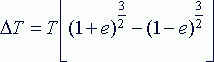
|
(3)
|
где T – период обращения планеты, а
ΔT – будет шириной орбиты, выраженной в терминах периодов. Назовем эту
величину «периодом ширины орбиты». При этом оказалось, что «период ширины
орбиты» связан с перодом обращения планеты, расположенной через одну орбиту
ближе к Солнцу, следующим соотношением:
где k – целое число, чаще всего, близкое
к единице, т.е. имеет место своеобразный резонанс, названный нами «кольцевым
резонансом» (см. табл. 3).
Таблица 3а

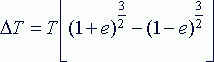
 Главная
Главная