|
|
|
|
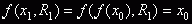 , таким
образом , таким
образом
|
|
|
|
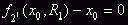
|
(5.1)
|
|
(б)
|
Цикл периода четыре:
|
|
|
|
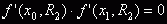 , где , где 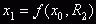
|
|
|
|
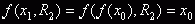 , таким
образом , таким
образом
|
|
|
|
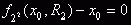
|
(5.2)
|
Для произвольных же 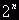 -циклов
справедливо выражение:
-циклов
справедливо выражение:
|
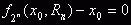
|
(6)
|
Уравнение (5.3) легко решается относительно параметра 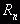 , например, с
помощью метода последовательных итераций Ньютона:
, например, с
помощью метода последовательных итераций Ньютона:
|
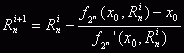
|
(6.1)
|
Здесь i - номер итерации. Таким образом, весь процесс
вычисления, скажем, константы 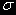 сводится к
нахождению таких значений параметра R, при которых бифуркационная диаграмма
пересекает линию
сводится к
нахождению таких значений параметра R, при которых бифуркационная диаграмма
пересекает линию 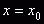 . Для этого
необходимо решить уравнение (6), проитерировав его
. Для этого
необходимо решить уравнение (6), проитерировав его 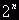 раз.
раз.
НА ВХОД ПОДАЕМ:
Начинаем итерировать функцию f cо следующего значения:
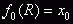
Итерируем производную функции начиная с 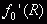
Начальные приближения двух значений параметра R: 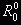 ,
, 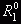
Разумное начальное приближение для постоянной : 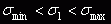
НА ВЫХОДЕ ПОЛУЧАЕМ:
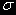
А весь процесс может быть описан следующими
выражениями:
Рекомендуем скачать другие рефераты по теме: реферат система управления, реферат мировые войны.
Предыдущая страница реферата |
1
2
3
4 |
Следующая страница реферата
 Главная
Главная