Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Решая это простое уравнение при естественных граничных условиях: u (1) = 1, u (0) = 0 , мы получим вероятность фиксации гена A1 в конечной популяции [1,3,6]:

u(P) = [1 - exp (- 4nsP)] [1 - exp (- 4ns)]-1 . (11)

Выражение (11) показывает, что если 4ns < < 1 , то имеет место нейтральная фиксация гена: u(P) » P , если 4ns > > 1, то отбирается предпочтительный ген A1 : u(P) » 1; размер популяции nc ~ (4s)-1 есть граничное значение, разделяющее области "нейтрального" и "селективного" отбора.

Итак, математические методы популяционной генетики описывают динамику частот генов в эволюционирующих популяциях. Детерминистические методы используются при описании динамики частот в среднем; стохастические методы учитывают флуктуации в популяциях конечной численности.

3. Молекулярная эволюция: теория нейтральности

Классическая теория популяционной генетики, содержательно основанная на синтетической концепции эволюции, интенсивно развивалась до 1960-х годов, до тех пор, пока не возникли трудности интерпретации экспериментальных данных молекулярной биологии. В лекции 1 я уже отмечал, в 1950-1960-х годах произошла революция в молекулярной биологии. Была определена структура ДНК, расшифрован генетический код, ученые установили общие принципы работы молекулярно-генетической системы живой клетки.

Интенсивные исследования молекулярной биологии привели к серьезным результатам, касающимся биологической эволюции: была оценена скорость аминокислотных замен в белках, а также получены оценки, характеризующие полиморфизм белков.

Анализируя экспериментальные данные, М.Кимура обнаружил, что когда он пытался объяснить эти эксперименты на основе селекции благоприятных мутаций путем Дарвиновского отбора, то возникли серьезные затруднения. В своей книге [6] Кимура подробно описывает идеи, послужившие основанием для изобретения теории нейтральности. Например, в некоторых своих оценках, основанных на Дарвинском отборе, он получил, что для объяснения экспериментальных данных нужно потребовать, чтобы каждая особь в процессе эволюции давала 22 000 потомков. И для того, чтобы проинтерпретировать данные по молекулярной эволюции белков, Кимура предложил теорию нейтральности [6,9].

Основное предположение этой теории состоит в следующем: на молекулярном уровне мутации (замены аминокислот или нуклеотидов) преимущественно нейтральны или слабо вредны (существенно вредные мутации также возможны, но они элиминируются из популяции селекцией). Это предположение согласуется с экспериментально наблюдаемой скоростью аминокислотных замен и с тем фактом, что скорость замен в менее важных частях белков значительно больше, чем для активных центров макромолекул.

Используя математические методы популяционной генетики, Кимура получил ряд следствий теории, которые находятся в довольно хорошем согласии с данными молекулярной генетики [6].

Математические модели теории нейтральности существенно стохастические, т.е. относительно малая численность популяции играет важную роль в фиксации нейтральных мутаций. См. примеры расчетов, приведенных выше.

Но если молекулярные замены преимущественно нейтральны, как возможна прогрессивная эволюция? Чтобы ответить на этот вопрос, Кимура использует концепцию дупликации генов, развитую С.Оно [10]. Согласно теории Кимуры, дупликация генных участков создает дополнительные, избыточные ДНК-последовательности, которые в свою очередь дрейфуют далее за счет случайных мутаций, предоставляя тем самым сырой материал, из которого могут возникать новые, биологически значимые гены (Рис.1).

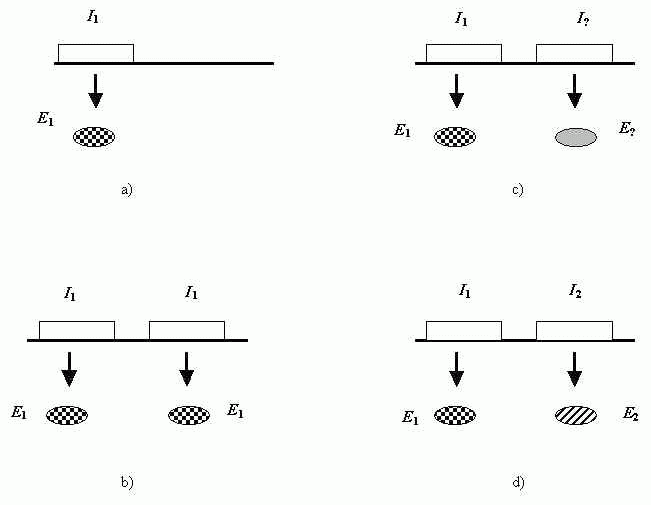
Рис. 1. Иллюстрация к механизму прогрессивной эволюции в теории нейтральности. Схема появления нового биологически значимого белка. Показаны участки ДНК ( Ii ) и кодируемые ими белки ( Ei ). a) ген I1 кодирует белок E1, b) дупликация гена I1, новый участок (справа) кодирует тот же белок E1, c) случайный дрейф правого участка, d) возникновение нового биологически значимого белка E2 кодируемого участком ДНК I2 .

Заключая наш сжатый обзор теории нейтральности, процитируем пять принципов этой теории [6]. Первые четыре из них – эмпирические, а пятый установлен теоретическим путем.

Скорость эволюции любого белка, выраженная через число аминокислотных замен на сайт в год, приблизительно постоянна и одинакова в разных филогенетических линиях, если только функция и третичная структура этого белка остаются в основном неизменными. Функционально менее важные молекулы и их части эволюционируют (накапливая мутационные замены) быстрее, чем более важные. Мутационные замены, приводящие к меньшим нарушениям структуры и функции молекулы (консервативные замены), в ходе эволюции происходят чаще тех, которые вызывают более существенное нарушение структуры и функции этой молекулы. Появлению нового в функциональном отношении гена всегда должна предшествовать дупликация гена. Селективная элиминация вредных мутаций и случайная фиксация селективно нейтральных или очень слабо вредных мутаций происходят в ходе эволюции гораздо чаще, чем положительный дарвиновский отбор благоприятных мутаций.

4. Другие модели, характеризующие общие закономерности эволюции

Теория нейтральности – одна из наиболее разработанных общих теорий эволюции. Однако есть ряд моделей и концепций, также характеризующих эволюцию на молекулярном уровне, которые в основном дополняют теорию нейтральности. Отметим наиболее известные из них.

В работах Д.С.Чернавского и Н.М.Чернавской [11,12] сделана оценка вероятности случайного формирования нового биологически значимого белка с учетом того, что в белке есть активный центр, в котором замены аминокислот практически недопустимы, и участки, свойства которых не сильно меняются при многих аминокислотных заменах. Там же сделана оценка количества возникающей в геноме информации при появлении нового белка. Полученная оценка указывает на то, что случайное формирование белка было вполне вероятно в процессе эволюции.

Интересна, хотя, по-видимому, не бесспорна, модель блочно-иерархического эволюционного отбора [13,14], согласно которой новые генетические тексты большой длины сначала случайно составляются из коротких текстов, оптимизированных в предыдущие эволюционные эпохи, а после составления оптимизируются. Модель блочно-иерархического эволюционного отбора критически проанализирована в [15].

Блочно-модульный принцип организации и эволюции молекулярно-генетических систем управления обосновывается В.А.Ратнером [16]. Согласно этому принципу эволюция генов, РНК, белков, геномов и молекулярных систем управления на их основе шла путем комбинирования блоков (модулей) снизу доверху, причем модулями, из которых составлялись вновь возникающие молекулярно-генетические системы, служили уже функционирующие макромолекулярные компоненты. По сравнению с моделью блочно-иерархического отбора блочно-модульный принцип более гибок и более реалистичен.

В модели "генов-мутаторов" [17] предполагается, что уровень мутаций может меняться и наследоваться, в результате чего при попадании популяции в новую среду, когда выгоден активный поиск новых свойств, уровень мутаций возрастает, а при длительном нахождении в постоянной среде, где важно сохранение уже найденных свойств, интенсивность мутаций падает.

Интересно проанализировать, как могли возникать достаточно нетривиальные системы обработки информации. Для простейших организмов (вирусов и бактерий) в качестве таковых можно рассматривать регулирование синтеза белков (функциональных и структурных элементов организма) в соответствии с определенной "программой". Например, в процессе онтогенеза фага Т4 происходит образование сложной пространственной структуры, в формировании которой участвуют несколько десятков белков, синтезируемых в соответствии с программой, закодированной геномом фага [18]. Иллюстративная модель эволюционного возникновения подобных "программ жизнедеятельности" предложена [19]. Согласно модели в процессе эволюционного формирования этих программ в генотип закладывается некоторая избыточность, которая приводит к тому, что при небольшой модификации генома часть блоков программ сохраняется. При введении в модель представлений о "генах-мутаторах" наблюдалось поведение, качественно сходное с явлением каскадного мутагенеза [20] – резким возрастанием интенсивности мутаций после дестабилизации генома.

В чрезвычайно интересном цикле работ С.Кауффмана с сотрудниками [21,22] исследуется эволюция автоматов, состоящих из соединенных между собой логических элементов. Отдельный автомат можно рассматривать как модель молекулярно-генетической системы управления живой клетки, при этом каждый логический элемент интерпретируется как регулятор синтеза определенного фермента. Модели Кауффмана позволяют сделать ряд предсказаний относительно "программ" жизнедеятельности клеток. В частности, продемонстрировано, что для одновременного обеспечения устойчивости и гибкости программы число входов логических элементов должно быть ограничено определенным интервалом, а именно составлять величину примерно равную 2-3. Для моделей Кауффмана разработаны эффективные методы анализа на базе статистической физики, эти модели получили широкую известность и исследовались рядом ученых. Подробнее основные результаты этой модели мы обсудим в следующей лекции.

Специальные термины:

Рекомендуем скачать другие рефераты по теме: изложение по русскому языку, шпоры на пятках.

Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата