Оптимальная частотно-временная фильтрация

канд. биологических наук М.П.Иванов, д-р техн. наук В.В.Кашинов

Санкт-Петербургский государственный университет

Методами обобщенного вариационного исчисления синтезирован частотно-временной фильтр, состоящий из перемножителя на известное опорное напряжение и включенного за ним стационарного фильтра. Показано, что корреляционный прием и согласованная фильтрация являются частными предельными случаями частотно-временного фильтра. При помощи понятия функции спектральной корреляции анализируется физический принцип работы частотно-временного фильтра. Показана возможность применения частотно-временного фильтра в спектральном дискриминаторе временных интервалов.

Структура некоторых приемных устройств, например, приемников американской спутниковой навигационной системы GPS, включает в себя коррелятор [1]. В корреляторе, являющемся оптимальным приемником при наличии белого шума (но не узкополосной помехи в виде расстроенной несущей [1]), осуществляется умножение входного процесса (сигнала и шума) на копию сигнала с последующим интегрированием. Поскольку существует еще возможность реализации оптимального приемника в виде согласованного фильтра, возникает вопрос, являются ли эти структуры оптимального приемника единственными?

Рассмотрим задачу частотно-временной фильтрации, которая заключается в умножении входного процесса на некоторое известное опорное напряжение (как и в перемножителе коррелятора), не уменьшающее энергию сигнала, и последующей линейной фильтрации (аналогично интегрированию в корреляторе) стационарным фильтром. Отклики частотно-временного фильтра на входной сигнал и шум можно представить в виде

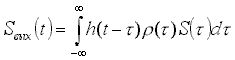 (1)

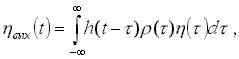и (2)

где - опорное напряжение; - импульсная переходная функция стационарного фильтра. Таким образом, ядра операторов (1,2) представлены в виде произведения k(t, t )=r (t )h(t-t ), где r - заданная известная функция, а h(t-t ) подлежит оптимизации.

При оптимизации будем использовать метод, разработанный в заметках [2-4]. В качестве критерия оптимальности выберем отношение сигнал-шум и представим значение полезного сигнала на выходе в момент максимума t0 с помощью фильтрующего свойства d - функции в виде линейного функционала

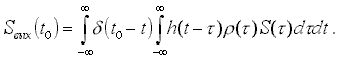 (3)

Момент t0 заранее неизвестен и принадлежит интервалу наблюдения T, а шум на выходе частотно-временного фильтра является нестационарным. Поэтому в качестве критерия оптимальности примем функционал I отношения пиковой мощности сигнала к средней по времени и по ансамблю мощности шума Pш на выходе фильтра

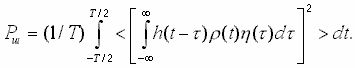 (4)

Здесь и в дальнейшем угловые скобки < T > обозначают усреднение по ансамблю.

Поскольку сомножитель h(t-t ) в ядре операторов (1) и (2) - разностный, можно использовать свойство свертки и записать

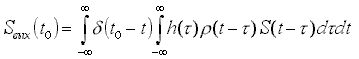 (5)

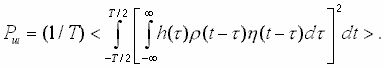и (6)

Таким образом, критерий оптимальности имеет вид

 (7)

где Sвых(t0) и Pш выражаются формулами (5) и (6). Здесь уже можно применить методы обобщенного вариационного исчисления [2-4]. Обобщенное уравнение Эйлера-Пуассона для функционала (7) имеет вид

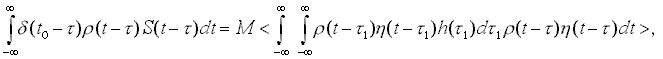 (8)

где M - коэффициент пропорциональности, не влияющий на вид коэффициента передачи фильтра.

Переходя к спектрам и обозначая соответствие функций и их преобразований Фурье;;;, получаем выражение для коэффициента передачи стационарной инерционной части оптимального частотно-временного фильтра

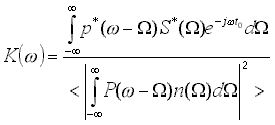 (9)

где * обозначает комплексное сопряжение.

При любом выборе опорного напряжения r (t), которому соответствует спектр P(W ), не уменьшающем энергию сигнала, и любой помехи, в том числе и узкополосной, выводящей GPS из строя [1], существует коэффициент передачи K(w ) оптимального стационарного фильтра h(t ). Мощность множества пар r (t) и K(w ) может быть больше мощности континуума [3]. Даже для рассмотренного простейшего случая все ограничения для r (t) и K(w ) не определены. Из существования решений для частного случая задачи [3] следует существование множества ядер k(x,t), доставляющих функционалу (7) экстремум, причем значения этого экстремума для каждого k(x,t) из этого множества - одинаковые. Решением оптимизационной задачи будет конструктивное описание этого множества оптимальных ядер. Если r (t)=const, т.е. перемножитель отсутствует, P(w -W )=d (w -W ) и получается согласованный фильтр; если r (t)=S(t), получается коррелятор.

Рекомендуем скачать другие рефераты по теме: реферат на тему рынок, контрольная работа 9.





1  2  3  4 | Следующая страница реферата