Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

Таким образом, и корреляционный прием, и согласованная фильтрация являются частными предельными случаями частотно-временной фильтрации. Опорное напряжение r (t) и переходную функцию фильтра h(t-t ) следует выбирать, исходя из удобства реализации. А для осуществления оптимального приема при белом шуме применение коррелятора или согласованного фильтра обязательным не является.

Решение сформулированной задачи заведомо неоднозначное. Для описания этого множества потребуется использовать понятие функции спектральной корреляции.

Представляя знаменатель в выражении (9) в виде двойного интеграла и меняя порядок интегрирования и статистического усреднения, получаем

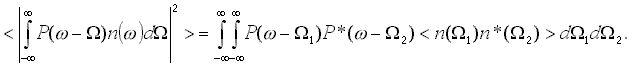 (10)

Обозначим B(w 1,w 2)=<n(w 1)n*(w 2)>; это выражение называется функция спектральной корреляции (ФСК) [5]. Если не учитывать свойства ФСК при мультипликативном воздействии на входной процесс, можно получить ошибочные результаты типа превышения потенциальной помехоустойчивости [6].

ФСК выражается через автокорреляционную функцию B(t1 ,t2 )

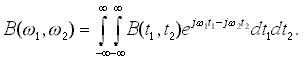 (11)

Средняя мгновенная мощность B(t1,t2) нестационарного процесса может быть выражена через ФСК

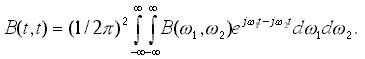 (12)

Таким образом, вклад в мгновенную мощность нестационарного процесса вносит не только составляющая с частотой w , но и все коррелированные с ней. Это означает, что средние энергетические характеристики нестационарного процесса не локализуемы по частоте, откуда следует невозможность представления энергетических характеристик нестационарного процесса с помощью однократных интегралов в частотной области.

Средняя по времени спектральная плотность мощности нестационарного процесса может быть выражена через ФСК

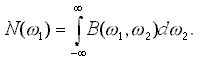 (13)

Спектральная плотность нестационарного процесса характеризует вклад составляющих в интервале частот (w + dw ) и всех коррелированных составляющих с другими частотами.

Для стационарных процессов автокорреляционная функция зависит только от разности моментов времени t = t1 vt2 , и в этом случае

 (14)

Для стационарных процессов все частотные составляющие некоррелированы.

При модуляции стационарного белого шума детерминированным опорным напряжением r (t) ФСК зависит только от разности частот

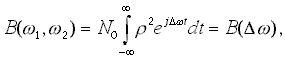 (15)

где D w = w 1 - w 2 . Например, при стробировании стационарного белого шума периодической последовательностью импульсов средняя по времени спектральная плотность уменьшается в скважность раз; это можно наблюдать на экране анализатора спектра. Но появляется свойство, которое нельзя наблюдать на экране анализатора спектра - между спектральными составляющими появляется корреляция.

Парадокс. Предположим, что осуществляется оптимальный прием отрезка периодической последовательности импульсов на фоне белого шума. Как известно, оптимальным в данном случае является согласованный гребенчатый фильтр. Теперь включим на входе оптимального гребенчатого фильтра стробирующее устройство (перемножитель на последовательность прямоугольных импульсов единичной амплитуды) так, чтобы импульсы сигнала проходили без искажений. Спектральная плотность шума на выходе стробирующего устройства уменьшится в скважность стробов раз. Казалось бы, что отношение сигнал-шум на выходе гребенчатого фильтра должно увеличиться, но оно и так было максимально возможным, поскольку фильтр оптимальный. Разрешить парадокс помогает появление корреляции между спектральными составляющими. Ясно, что суммирование "гребенок" фильтра со сфазированными гармоническими составляющими сигнала и коррелированными составляющими шума результирующее отношение сигнал-шум не повысит.

Частотно-временная фильтрация может с успехом использоваться в спектральных дискриминаторах временных интервалов [7]. В некоторых радиоканалах, например, телеметрических каналах сверхдальней космической связи или GPS [1], отношение сигнал-шум оказывается Pс /Pш << 1. В таких каналах можно использовать временное уплотнение телеметрической информации путем передачи периодически повторяющихся пар импульсов для накопления, в интервале между которыми и заключается сообщение.

Способ дискриминирования отклонения временного интервала от заданного значения между импульсами периодической двухимпульсной последовательности (рис.1) заключается в следующем [7]. Огибающая амплитудного спектра (рис.2) такой последовательности находится в жесткой связи с интервалом между импульсами; сравнивая амплитуды определенных гармоник, можно судить о величине и знаке отклонения интервала t инт между импульсами пары от заданного значения t 0 .

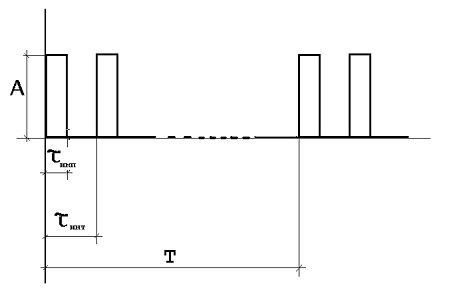
Рис. 1. Периодическая двухимпульсная последовательность.

Разложим временной процесс (рис.1) в тригонометрический ряд Фурье, т. е. вычислим спектр сигнала. При этом выражение для амплитуды n-й гармоники примет вид

Рекомендуем скачать другие рефераты по теме: реферат на тему рынок, контрольная работа 9.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата