Claw.ru | психология, педагогика | Возможности использования элементов теории вероятностей и статистики на уроках математики в начальной Возможности использования элементов теории вероятностей и статистики на уроках математики в начальной школе | Категория реферата: психология, педагогика | Теги реферата: здоровый образ жизни реферат, реферат финансовый | Добавил(а) на сайт: Kobyl'skih. Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата	(2,5)	(3, 5)	(4, 5)	(5, 5)	(6, 5)
(1, 6)	(2,6)	(3, 6)	(4, 6)	(5, 6)	(6, 6)

Пример 2. Сколько элементарных исходов благоприятствует событию “на обоих кубиках выпало одинаковое число очков” при подбрасывании двух игральных кубиков.

Решение. Этому событию благоприятствуют 6 элементарных исходов (см. табл. 1): (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6).

Пример 3. Подбрасывается два игральных кубика. Какому событию благоприятствует больше элементарных исходов: “сумма выпавших очков равна 7”, “сумма выпавших очков равна 8”?

Решение. Событию “сумма выпавших очков равна 7” благоприятствуют 6 исходов (в табл. 1 выделены цветом). Событию “сумма выпавших очков равна 8” благоприятствует 5 исходов: (2, 6), (3, 5), (4, 4), (5, 3), (6, 2). Ответ ясен.

Кстати говоря, можно предложить учащимся и другое задание: подсчитать, сколько элементарных исходов благоприятствует событиям “сумма очков на кубиках равна 2”, “сумма очков на кубиках равна 3” и т. д., и эти результаты отметить на координатной плоскости, с которой учащиеся начальных классов знакомы.

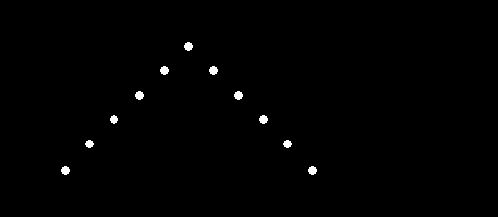
Ðèñ. A

Пример 4. Подбрасывается три игральных кубика, подсчитываются суммы очков, выпавших на них. Сколькими способами можно получить в сумме 5 очков; 6 очков?

Решение. Получить в сумме 5 очков можно шестью способами: (1; 1; 3)[4] , (1; 3; 1), (3; 1; 1), (1; 2; 2), (2; 1; 2), (2; 2; 1). Получить в сумме 6 очков можно десятью способами (1; 1; 4), (1; 4; 1), (4; 1; 1), (1; 2; 3), (1; 3; 2), (2; 1; 3), (2; 3; 1), (3; 1; 2), (3; 2; 1), (2; 2; 2).

I. 3. Классическое определение вероятности

Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события A обозначают через P(A) (здесь P — первая буква французского слова probabilite — вероятность):

,

ãäå m — число элементарных исходов, благоприятствующих событию A; n — число всех равновозможных элементарных исходов опыта, образующих полную группу событий.

Это определение вероятности называют классическим. Оно возникло на начальном этапе развития теории вероятностей.

Рекомендуем скачать другие рефераты по теме: отечественная история шпаргалки, реферат по литературе.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата