Claw.ru | психология, педагогика | Возможности использования элементов теории вероятностей и статистики на уроках математики в начальной Возможности использования элементов теории вероятностей и статистики на уроках математики в начальной школе | Категория реферата: психология, педагогика | Теги реферата: здоровый образ жизни реферат, реферат финансовый | Добавил(а) на сайт: Kobyl'skih. Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата	бб	бб	бб	бб
7(б)	бч	бч	бч	бб	бб	бб	бб

Нетрудно подсчитать, что равновозможных исходов 49. Вероятность появления двух черных шаров равна 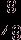, двух белых — 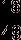, шаров разных цветов — .

Задача 3. Найдите вероятности того, что при двойном испытании как в предыдущей задаче: а) вынут по крайней мере один черный шар; б) вынут хотя бы один белый шар; в) первым вынут черный шар; г) последним вынут белый шар.

Обсуждение. Для решения воспользуемся таблицей из предыдущей задачи. Вероятности равны: а) ; б) ; в) ; г) .

I. 4. О смысле формулы вероятности события

Мы вывели эту формулу с помощью некоторых утверждений. Можно ли утверждать, что мы ее доказали, как доказывают теоремы? Нет, конечно. Мы построили модель реального явления (вынимание шаров из урны). Модель подтверждается фактами и экспериментами. А с математической точки зрения формула есть определение вероятности. И эта формула связывает модель с реальным миром.

Задача 4. Брошены независимо друг от друга две правильные игральные кости. Найти вероятности того, что сумма очков на верхних гранях: а) меньше 9; б) больше 7; в) делится на 3; г) четна.

Обсуждение. При бросании двух костей имеется 36 равновозможных исходов, поскольку имеется 6´6 = 36 пар, в которых каждый элемент — целое число от 1 до 6. Составим таблицу (табл. 3), в которой слева число очков на первой кости, вверху — на второй, а на пересечении строки и столбца стоит их сумма.

Òàáë. C