Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата

Задача 9. Бросают три игральные кубика. Что вероятнее: сумма очков на верхних гранях равна 11 или эта сумма равна 12? Каковы вероятности этих событий?[6]

Обсуждение. Прежде всего найдем, сколькими способами можно представить 11 и 12 в виде суммы трех натуральных слагаемых, каждое из которых не превосходит 6. Будем выписывать суммы в порядке возрастания слагаемых. Начнем с 11. Если наименьшее слагаемое — 1, то 11 = 1 + 4 + 6 либо 11 = 1 + 5 + 5. Если 2, то 11 = 2 + 3 + 6 либо 11 = 2 + 4 + 5. Если 3, то 11 = 3 + 4 + 4 либо 11 = 3 + 3 + 5. Этими случаями (6) исчерпываются все представления 11 в виде суммы трех чисел, нанесенных на грани кубиков. Число 12 можно представить шестью способами: 12 = 1 + 5 + 6 = 2 + 4 + 6 = 2 + 5 + 5 = 3 + 3 + 6 = 3 + 4 + 5 = 4 + 4 + 4. Шевелье де Мере заключил отсюда, что 12 в качестве суммы будет встречаться столь же часто, как и 11. Однако результаты многих игр показали, что, вопреки расчетам де Мере, 11 встречается чаще. Именно тогда Мере усомнился в теории вероятностей и обратился к Паскалю за разъяснениями. Паскаль решил задачу. Оказалось, что теория вероятностей верна, а рассуждения де Мере ошибочны. Шевалье не учел, что. скажем, 4 + 4 + 4 может выпасть одним способом: на всех трех кубиках 4, а 1 + 4 + 6 — многими: на первом — 1, на втором — 4, на третьем — 6 или на первом — 6, на втором — 4, на третьем — 1 и т. д.

Найдем вероятности того, что сумма очков на верхних гранях равна 11, и того, что эта сумма равна 12. При бросании трех кубиков имеется 6´6´6 = 216 равновозможных исходов. Событие “сумма очков равна 11” может осуществиться одним из шести способов: “выпали числа 1, 4, 6”, “выпали числа 1, 5, 5” и т. д. Посчитаем, сколько для каждого из этих способов имеется благоприятных исходов. Событию “выпали 1, 4, 6” соответствуют 6 исходов, которые можно записать так: 146 (на первом кубике на верхней грани 1, на втором — 4, на третьем — 6), 164, 416, 461, 614, 641. Точно так же 6 исходов благоприятны для любого способа представления суммы в виде трех различных слагаемых. Событию “выпали 1, 5, 5” соответствует три исхода: 155, 551, 515. Всего для события “сумма очков равна 11” благоприятны 6 + 3 + 6 + 6 + 3 + 3 = 27 исходов. А событию “сумма очков равна 12” благоприятны 6 + 6 + 3 + 3 + 6 + 1 = 25 исходов, поскольку представлению 4 + 4 + 4 соответствует только один исход — 444. Итак, вероятность того, что сумма очков равна 11, есть 27/216 = 1/8, а вероятность того, что эта сумма равна 12, есть 25/216 = 1/8 - 1/108 < 1/8. Решение этой задачи показывает, как важно правильно выделить равновозможные исходы.

Задача 10. В шахматном турнире участвуют 8 игроков. Номера шести игроков распределяются по жребию. Номер определяет положение игрока в турнирной лестнице. Предположим, что лучший игрок всегда побеждает второго по мастерству, а тот в свою очередь побеждает всех остальных. Второе место занимает проигравший в финале. Какова вероятность того, займет второй по мастерству игрок?

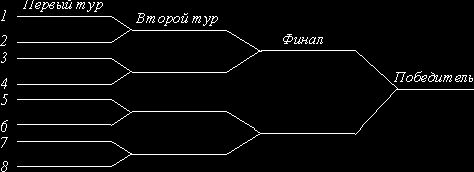
Ðèñ. B

Обсуждение. Второй по мастерству игрок занимает второе место тогда и только тогда, когда он находится в той половине турнирной лестницы (верхней или нижней), в которой нет первого по мастерству игрока, поскольку в противном случае второй проиграет первому ранее финала. Поскольку имеется 7 ступеней турнирной лестницы (кроме ступени, занятой первым по мастерству игроком), которые может занимать второй по мастерству игрок, все эти исходы равновозможны, а 4 из них являются благоприятными для выхода в финал, то искомая вероятность равна 4/7.

Задача 11. Король Артур проводит рыцарский турнир, в котором порядок состязания определяется жребием (по турнирной лестнице). Среди восьми рыцарей, одинаково искусных в ратном деле, два близнеца. Какова вероятность того, что они встретятся в поединке?

Обсуждение. Обозначим близнецов A и B. Если A и B входят в одну пару в турнирной лестнице, что происходит с вероятностью 1/7 (для B равновозможны 7 мест, не занятых A), то близнецы заведомо встречаются в первом же туре. Вероятность того, что B находится в соседней паре, равна 2/7. В этом случае близнецы встречаются во втором туре) только тогда, когда они оба выиграют поединки первого тура, что происходит с вероятностью 1/4. Значит, вероятность события “близнецы встречаются во втором туре” равна 2/7´1/4 = 1/14. Наконец, вероятность того, что B находится в другой половине турнирной лестницы, равна 4/7, и в этом случае вероятность встречи равна 1/4´1/4 = 1/16, поскольку оба должны победить в обоих турах; вероятность события “близнецы встречаются в финале” есть 4/7´1/16 = 1/28. Все возможности перечислены, вероятность встречи в одном из туров есть сумма вероятностей встреч в первом, втором турах и финале, т. е. 1/7 + 1/14 + 1/28 = 1/4.

Задача 12. Задача о разделе ставки (вторая задача Шевалье де Мере, предложенная Паскалю). Подбрасывается монета. Первый игрок “набирает” гербы, а второй — решки. Тот, кто первым наберет три единицы, забирает ставку. Игра была прервана, когда у первого игрока имелось два герба, а у второго — одна решка. Ставка должна быть разделена пропорционально шансам на выигрыш. Как ее разделить?

Обсуждение. Полезно ввести опыт, состоящий в двукратном бросании монеты. Из четырех равновозможных исходов ГР (при первом бросании выпал герб, при втором — решка), ГГ, РГ, РР, в первых трех победа принадлежит первому игроку (в первых двух случаях в самой игре монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку.

Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы)

Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при одних и тех же условиях, а детям предлагают указать результат. Потом условия эксперимента изменяют.

Приведем примеры игр и заданий, которые можно использовать при знакомстве младших школьников с основными понятиями теории вероятностей [2, 56; 14, 98].

1. Эксперимент, помогающий подвести младших школьников к понятиям: невозможное событие, достоверное событие, а в отношении случайных событий — установить градации: более вероятное событие, менее вероятное событие.

Оборудование: мешок и 9 шаров — 3 красных, 3 белых и 3 зеленых.

Описание эксперимента. Учитель обращается к ребятам:

— Вы, конечно, знаете, что Буратино очень любит кукольные спектакли, но у него часто не бывает денег, чтобы попасть в театр. Однажды продавец билетов согласился дать Буратино билет, если он верно ответит на вопрос: “В мешке имеется 3 красных, 3 белых и 3 зеленых шара. Сколько шаров нужно вынуть из мешка, чтобы наверняка иметь шары трех цветов?” Помогите Буратино дать правильный ответ.

Дети будут предлагать разные значения, но им необходимо обосновать свой выбор, проводя эксперименты. В результате они должны прийти к следующим выводам:

— если вынуть 7, 8, 9 шаров, наверняка будут шары трех цветов;

— если вынуть 3, 4, 5 или 6 шаров, то возможно, но не обязательно будут шары трех цветов;

— если вынуть 1 или 2 шара, то невозможно получить шары трех цветов.

Целесообразно исследовать, в каком из случаев имеется наибольшая возможность получить шары трех цветов — если вытащить 3, или 4, или 5, или 6 шаров. Можно ввести и термины более вероятно, менее вероятно.

2. Опыты с пятью монетами. С помощью этих экспериментов можно научить ребенка навыку выводить закономерности при проведении опытов.

Рекомендуем скачать другие рефераты по теме: отечественная история шпаргалки, реферат по литературе.





Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата