Claw.ru | психология, педагогика | Возможности использования элементов теории вероятностей и статистики на уроках математики в начальной Возможности использования элементов теории вероятностей и статистики на уроках математики в начальной школе | Категория реферата: психология, педагогика | Теги реферата: здоровый образ жизни реферат, реферат финансовый | Добавил(а) на сайт: Kobyl'skih. Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата	Сколько раз все карточки оказались на своем месте?
4	Сколько раз две карточки оказалась на своем месте?
5	Сколько раз три карточки оказалась на своем месте?
6	Сколько раз четыре карточки оказалась на своем месте?

Затем повторить опыт еще 10 раз. На самом деле мы имеем уже 20 опытов, которые опять заносим в таблицу и вычисляем относительную частоту при n = 20. Проделав опыт, например, 100 раз, можно определить приближенное значение вероятности для каждого исхода.

А как определить вероятность на множестве элементарных событий? Далее можно привести формулу классической вероятности (выше мы ее предлагали).

Элементарным, как это видно из самого названия, является самое простое событие, которое нельзя разложить на другие события.

Например, выпадение на кубике четного числа — событие не элементарное. Оно раскладывается на три события: выпала двойка, выпала четверка, выпала шестерка. А вот выпадение каждого числа как раз и есть элементарное событие. При бросании кубика получаем множество из 6-ти элементарных событий. Событию “выпадание четного числа” соответствует подмножество из элементов 2, 4, 6 (мера этого подмножества M = 3). Событию “выпадание числа больше двух” соответствует подмножество из четырех элементов.

Обозначим множество элементарных событий греческой буквой  (омега). Тогда можем записать:

.

Пример. Пусть событие A — выпадание на кубике четного числа; M(A) = 3. Здесь  — множество всех возможных выпаданий; M() = 6. Значит, .

Пример. Возьмем мешок с 10 шариками (4 красных, 3 желтых, 3 синих). Ты наугад вынимаешь из мешка шарик. Множество элементарных событий состоит из 10-ти элементов; каждый элемент — вынимание одного шарика (M() = 10). Множество элементарных событий разбито здесь на три подмножества: красное (M(K) = 4), желтое (M(Ж) = 3), синее (M(С) = 3). Вероятность вытянуть с закрытыми глазами синий шарик определяется по формуле:

.

Аналогично без труда находятся вероятности P(K) и P(Ж).

Пример. Возьмем колоду игральных карт. Элементарное событие — вытягивание карты из колоды. Всего карт 36: 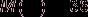. Изобразим множество  в виде таблицы:

Òàáë. F