|
109,2
|
12890,0
|
3,3
|
-179,5
|
|
2002
|
17001
|
105,2
|
14757,0
|
3,8
|
-219,0
|
|
2003
|
18566
|
109,6
|
17331,0
|
3,5
|
-257,8
|
|
2004
|
18960
|
112,1
|
22241,0
|
3,0
|
-334,2
|
|
2005
|
19424
|
102,7
|
30136,0
|
2,4
|
-477,2
|
Для наглядного аналізу даних
приведемо значення факторів та результуючого показника на рисунках 3.1, 3.2, 3.3, 3.4 та 3.5.
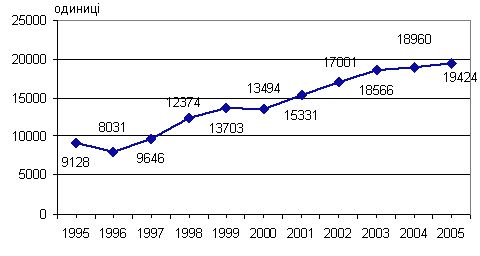
Рисунок 3.1 - Кількість малих
підприємств у Дніпропетровській області, одиниць (Y)
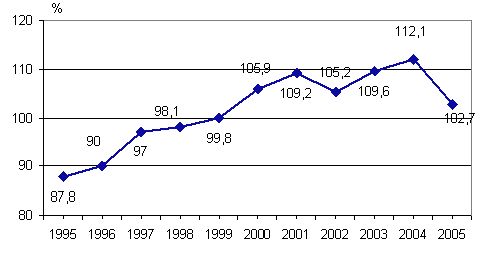
Рисунок 3.2 - Темпи зростання ВВП
до попереднього року в Україні у порівняних цінах, % (X1)
На рисунках 3.1 та 3.1 напрямок
розвитку кількості малих підприємств Дніпропетровської області та темпи
зростання ВВП до попереднього року в Україні у порівняних цінах однаково
прямують до збільшення.
Найбільший приріст кількості
малих підприємств Дніпропетровської області спостерігався у 1996 – 2003 роках, у 2003 – 2005 збільшення дещо уповільнилось. Так само темпи зростання ВВП були
найбільшими, але з 1996 до 2001 року. Та в останній 2005 рік показник
зменшився.
З графічного зображення факторів
на рисунку 3.1 та 3.2 видно, що вони мають приблизно лінійну тенденцію до
зростання.
Наступний показник - доходи
населення Дніпропетровської області – також збільшується. Приблизно характер
показника може описувати парабола другого порядку. Але вигін даних невеликий, тому можна говорити про лінійне збільшення показника.
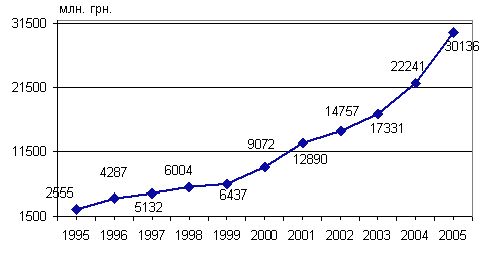
Рисунок 3.3 - Доходи населення
Дніпропетровської області, млн. грн. (X2)
Останні два фактори - рівень
безробіття та перевищення заробітної плати на малих підприємствах над середньою
по області у працівників, зображені на рисунках 3.4 та 3.5.
Фактори мають протилежні
тенденції до попередніх факторів. Показники зменшуються.
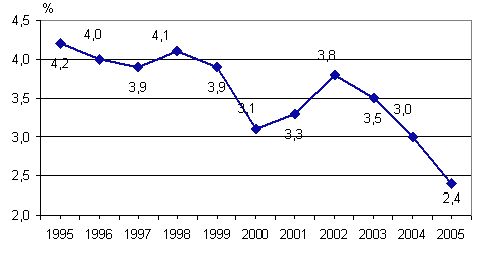
Рисунок 3.4 - Рівень
зареєстрованого безробіття населення (на кінець року), % (X3)
Відхилення по заробітній платі
вирізняється поміж іншими факторами тим, що воно постійно від’ємне.
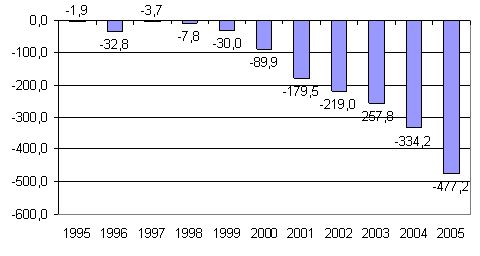
Рисунок 3.5 - Відхилення
середньомісячної заробітної плати малих підприємств та середньомісячної
заробітної плати працівників у Дніпропетровській області, грн. (X4)
Можна також дуже приблизно з
огляду на вихідні дані останніх двох показників говорити, що вони змінюються
лінійно.
У даному розділі ми будуємо дві
моделі з наявних факторів. Припускаємо, що між ними та результатом існує
лінійний зв’язок.
Перша модель має вигляд:
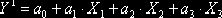 , (2.19)
, (2.19)
де 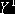 - кількість малих підприємств Дніпропетровської
області;
- кількість малих підприємств Дніпропетровської
області;
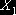 - Темпи зростання ВВП України до попереднього
року у порівняних цінах, %;
- Темпи зростання ВВП України до попереднього
року у порівняних цінах, %;
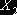 - Доходи населення Дніпропетровської області, млн. грн.;
- Доходи населення Дніпропетровської області, млн. грн.;
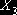 - Рівень зареєстрованого безробіття населення
Дніпропетровської області (на кінець року), %;
- Рівень зареєстрованого безробіття населення
Дніпропетровської області (на кінець року), %;
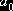 ,
, 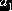 ,
,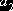 та
та 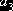 - коефіцієнти першої моделі.
- коефіцієнти першої моделі.
У другу модель замість рівня
зареєстрованого безробіття населення Дніпропетровської області введемо різницю
у заробітній платні на малих підприємствах від середньої заробітної плати
працівників у Дніпропетровській області (грн.). Друга модель має вид:
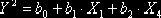 , (2.20)
, (2.20)
де 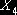 - різниця у заробітній платні на малих
підприємствах та середньої заробітної плати працівників у Дніпропетровській
області, грн;
- різниця у заробітній платні на малих
підприємствах та середньої заробітної плати працівників у Дніпропетровській
області, грн;
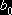 ,
, 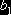 ,
,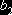 та
та 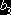 - коефіцієнти другої моделі.
- коефіцієнти другої моделі.
Перевіримо наявність
мультиколінеарності між факторами 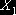 ,
, 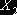 та
та 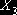 першої моделі. Для цього за тестом
Фарара-Глобера перевіримо значення
першої моделі. Для цього за тестом
Фарара-Глобера перевіримо значення 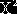 , використовуючи формулу (2.15).
, використовуючи формулу (2.15).
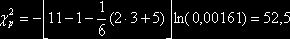
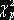 значно
перевищує
значно
перевищує 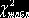 : 52,5 >
15,5 (при
: 52,5 >
15,5 (при 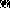 = 0,05 та
= 0,05 та  = 11-3 = 8). Тобто, в масиві пояснюючих
змінних першої моделі мультиколінеарність існує.
= 11-3 = 8). Тобто, в масиві пояснюючих
змінних першої моделі мультиколінеарність існує.
Для факторів другої моделі 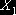 та
та 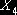 значення
значення 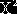 становить:
становить:
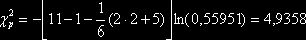
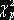 значно менший
значно менший 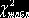 : 4,9358 <
16,9 (при
: 4,9358 <
16,9 (при 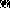 = 0,05 та
= 0,05 та  = 11-2 = 9). Тобто, в масиві пояснюючих
змінних другої моделі мультиколінеарність не існує.
= 11-2 = 9). Тобто, в масиві пояснюючих
змінних другої моделі мультиколінеарність не існує.
Розрахуємо коефіцієнти кореляції
Пірсона між факторами та порівняємо їх із сукупним коефіцієнтом кореляції.
Застосуємо формулу:
 , (2.21)
, (2.21)
де с – елементи матриці С, зворотної до кореляційної: С = r -1 .
Коефіцієнт кореляції ми можемо
порахувати, оскільки припускаємо, що між факторами існує лінійний зв’язок.
Наведемо розраховані парні та частинні коефіцієнти кореляції у таблиці 3.3.
Таблиця 3.3 – Коефіцієнти парної
та частинної кореляції та рівні їх значущості при 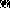 =0,01.
=0,01.
|
|
|
Y
|
X1
|
X2
|
X3
|
X4
|
|
Y
|
Коефіцієнт
парної кореляції
|
1,000
|
,854
|
,904
|
-,742
|
-,890
|
|
|
Значимість
|
,
|
,001
|
,000
|
,009
|
,000
|
|
X1
|
Коефіцієнт
парної кореляції
|
,854
|
1,000
|
,670*
|
-,649*
|
-,647*
|
|
|
Значимість
|
,001
|
,
|
,024
|
,031
|
,031
|
|
X2
|
Коефіцієнт
парної кореляції
|
,904
|
,670*
|
1,000
|
-,877
|
-,993
|
|
|
Значимість
|
,000
|
,024
|
,
|
,000
|
,000
|
|
X3
|
Коефіцієнт
парної кореляції
|
-,742
|
-,649*
|
-,877
|
1,000
|
,861
|
|
|
Значимість
|
,009
|
,031
|
,000
Рекомендуем скачать другие рефераты по теме: бесплатные рефераты и курсовые, сочинение на тему зимой.
Предыдущая страница реферата | 34
35
36
37
38
39
40
41
42
43
44 | Следующая страница реферата
|
|






 , (2.21)
, (2.21) Главная
Главная