Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

причем в числителе ставится большая из двух дисперсий. Расчетное F сравнивают с _____________, которое находят из таблиц, для степеней свободы  _____________________________________где N1 - число элементов выборки, по который вычислена _______ .

N2 - число элементов выборки, по которым получена оценка дисперсии ________.

Если F<Fкр     , то принимается нулевая гипотеза о равенстве генеральных дисперсий _________________     при принятом уровне значимости q.

На рис. 1.3 показаны кривые распределения _____. Зачернена об­ласть критических значений F .

На практике задача сравнения дисперсий возникает, если требуется сравнить .точность приборов, инструментов или методов измерений. Предпочтительнее тот прибор, инструмент или метод, который обеспечи­вает наименьшее рассеяние результатов измерений, т.е. наименьшую дис­персию.

.     .

Кривые F-распределения Фишера

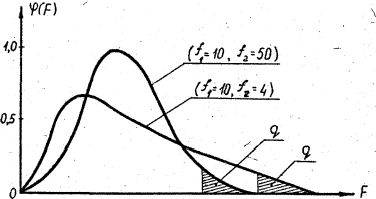
Рис.1.3

Если окажется, что нулевая гипотеза справедлива, т.е. генераль­ные дисперсии одинаковы, то различие несмещенных оценок дисперсий незначимо и объясняется случайными причинами, в частности  случайным отбором объектов выборки. Например, если различие несмещенных оценок дисперсий результатов измерений, выполненных двумя приборами, оказа­лось незначимым, то приборы имеют одинаковую точность.

Если нулевая гипотеза будет отвергнута, т.е. генеральные диспер­сии неодинаковы, то различие несмещенных оценок дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны. Например, если разли­чие _________________   результатов измерений, произведенных двумя приборами, оказалась значимым, то точность приборов различна.

1.8. Критерий Кохрэна

G -критерий Kохрэна применяется для оценки однородности несмещенных оценок дисперсий, вычисленных по одинаковому чис­лу N наблюдений. При этом генеральные совокупности должны быть распределены нормально. Критерий формируется как отношение максимальной из сравниваемых оценок дисперсий к сумме всех K дисперсий;

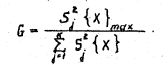
Если G<Gкр=Gq,f1,f2 , то оценки дисперсий признаются однородными или, другими словами, различаются незначимо. В этом слу­чае с уровнем значимости q ммнимается нулевая гипотеза, состоящая в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: _____________________________________________.Числа степе­ней свободы числителя f1 и знаменателя f2 определяются условиями

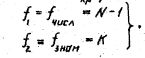
Если требуется оценить генеральную дисперсию, то при условии од­нородности оценок дисперсий целесообразно принять в качестве ее оцен­ки среднее арифметическое несмещенных оценок дисперсий

1.9. Критерий Пирсона

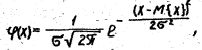Нормальный закон распределения характеризуется плотностью вероят­ности вида

где M{X}, ____ — соответственно математическое ожидание и диспер­сия случайной величины. согласованности изучаемого распределения с нормальным

Для проверки гипотезы о соответствии, экспериментального закона распределения случайной величины нормальному применяют критерий Пир­сона или, как его иначе называют, критерий X2 (хи-квадрат),так как принятие и отклонение гипотезы основаны на X2 -распределении.

Использование критерия Пирсона основано на сравнении эмпиричес­ких (наблюдаемых) ___ и теоретических (вычисленных в предположении нормального распределения) _____ частот. Обычно ____ и  _____ различны.

Возможно, что расхождение случайно (незначимо) и объясняется малым числом наблюдений, способом их группировки Или другими причина­ми. Возможно, что расхождение частот неслучайно (значимо) и объясня­ется тем, что теоретические частоты вычислены, исходя из неверной ги­потезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный ранее вопрос. Однако, как и любой статистический критерий, он не доказывает справедливость гипотезы, а лишь устанавливает при принятом уровне значимости q ее согласие или несогласие с данными наблюдений.

Пусть по выборке объема ___ получено эмпирическое распределение.

Допустим, в предположении нормального распределения генеральной совокупности, вычислены теоретические частоты _____. При уровне значимости q требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

Рекомендуем скачать другие рефераты по теме: скачати реферат, культура реферат.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата