Дифференциальные уравнения неустановившегося движения воздуха по рудничным воздуховодам

Асп. Баглей С.Г., проф. Воронин П.А.

Кафедра теоретической электротехники и электрических машин.

Северо-Кавказский государственный технологический университет

Произведен вывод нелинейной системы дифференциальных уравнений в частных производных для расчета давления и скорости движения воздуха по воздуховодам при его нестационарном квадратичном движении. При этом использованы: формула Дарси-Вейсбаха – формула потерь давления на трение; второй закон Ньютона для определения инерционных потерь давления и уравнение неразрывности движения потока воздуха. Приведен пример расчета неустановившегося расхода воздуха в коротком воздуховоде при подаче на его вход постоянного давления.

Переходные процессы движения воздуха в трубопроводах могут продолжаться относительно долго и существенно влиять на работу вентиляторной установки, особенно на работу электродвигателя. Особое значение имеют переходные процессы воздушного потока в горных выработках и трубопроводах, в которых время распространения звука от одного конца к другому значительно больше времени пуска двигателя вентилятора или времени открытия задвижки.

Задача настоящих исследований состоит в том, чтобы дать методику получения дифференциальных уравнений движения воздуха по трубопроводам, удобных для практического их решения.

Впервые связь между потерями напора на трение и средней по сечению воздуховода скоростью (или расходом воздуха) выявлена в XVIII в., когда была получена формула Дарси – Вейсбаха [1, стр.170; 2, стр.130].

Потеря давления на трение при движении воздуха по трубам по формуле Дарси – Вейсбаха имеет вид:

 (1)

где ∆ – обозначение разности; р – давление (Па = Н/м2) [3];  – коэффициент гидродинамического трения (б/р) [1]; D – внутренний диаметр трубы (м); v – средняя по поперечному сечению воздухопровода скорость движения воздуха (м/с);  – объемный вес воздуха (Н/м3) при давлении окружающей среды [1, 3]; – ускорение силы тяжести (м/с2); ∆х – длина участка воздуховода (м).

Для преобразования уравнения (1) учтем нижеследующее. Объемный вес воздуха (удельный вес) (Н/м3) выражается формулой [3]:

 (2)

где  – плотность воздуха (кг/м3) при давлении окружающей среды [3]. Соотношение между гидравлическим радиусом Rг и диаметром D круглой трубы имеет вид:

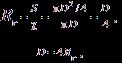 (3)

где S – площадь поперечного сечения воздухопровода (потока) (м2),

χ – смоченный периметр воздуховода (м).

Рис. 1. Конструктивная схема воздуховода. Условия равновесия

давлений (а) и скоростей (б) на бесконечно малом участке

воздуховода длиной d x.

В формуле (1) устремим длину трубы ∆х к бесконечно малой величине dx. Тогда получим дифференциал потерь давления. Кроме этого, подставим в это выражение значения формул (2) и (3). В результате получим выражение потерь давления на трение на бесконечно малом участке воздуховода (рис.1,а), т. е.

 (4)

Здесь давление р(x,t) и скорость v(x,t) являются функциями двух переменных – расстояния от начала воздуховода до рассматриваемого сечения его (х) и времени от начала переходных процессов до рассматриваемого момента (t).

При неустановившемся движении воздуха в воздуховодах существуют и инерционные потери давления. По второму закону Ньютона [4] инерционные потери давления на бесконечно малой длине воздуховода выражаются следующим дифференциалом (рис.1,а):

 (5)

В соответствии с условием равновесия давлений на границах бесконечно малого участка воздуховода dx (рис.1,а) можно записать

Рекомендуем скачать другие рефераты по теме: изложение лицей, реферати українською мовою.





1  2  3  4  5 | Следующая страница реферата