Абстрактная теория групп I.Понятие абстрактной группы 1.Понятие алгебраической операции.

Говорят, что на множестве X определена алгебраическая операция (* ), если каждой упорядоченной паре элементов 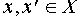поставлен в соответствие некоторый элемент 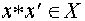называемый их произведением.

Примеры.

Композиция перемещений на множествах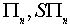 является алгебраической операцией. Композиция подстановок является алгебраической операцией на множестве 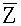всех подстановок степени n. Алгебраическими операциями будут и обычные операции сложения, вычитания и умножения на множествах Z,R,C соответственно целых, вещественных и комплексных чисел. Операция деления не будет алгебраической операцией на этих множествах, поскольку частное 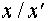не определено при 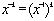. Однако на множествах 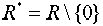, 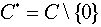это будет алгебраическая операция. Сложение векторов является алгебраической операцией на множестве . 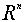Векторное произведение будет алгебраической операцией на множестве 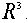. Умножение матриц будет алгебраической операцией на множестве всех квадратных матриц данного порядка. 2.Свойства алгебраических операций. 1. Операция (*) называется ассоциативной, если .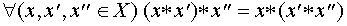

Это свойство выполняется во всех приведенных выше примерах, за исключением операций вычитания ( и деления) и операции векторного умножения векторов. Наличие свойства ассоциативности позволяет определить произведение любого конечного множества элементов. Например, если 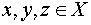, 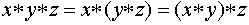. В частности можно определить степени с натуральным показателем: 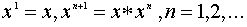. При этом имеют место обычные законы: , .

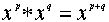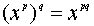2. Операция (*) называется коммутативной, если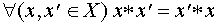

В приведенных выше примерах операция коммутативна в примерах 3 и 4 и не коммутативна в остальных случаях. Отметим, что для коммутативной операции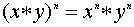

3. Элемент 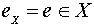называется нейтральным для алгебраической операции (*) на множестве X, если 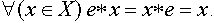. В примерах 1-6 нейтральными элементами будут соответственно тождественное перемещение, тождественная перестановка, числа 0 и 1 для сложения и умножения соответственно (для вычитания нейтральный элемент отсутствует !), нулевой вектор, единичная матрица. Для векторного произведения нейтральный элемент отсутствует. Отметим, что нейтральный элемент (если он существует) определен однозначно. В самом деле, если 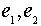- нейтральные элементы, то 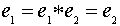. Наличие нейтрального элемента позволяет определить степень с нулевым показателем: .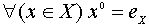

4. Допустим, что для операции (*) на X существует нейтральный элемент. Элемент 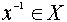называется обратным для элемента 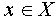, если 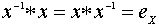. Отметим, что по определению 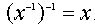. Все перемещения обратимы также как и все подстановки. Относительно операции сложения все числа обратимы, а относительно умножения обратимы все числа, кроме нуля. Обратимые матрицы - это в точности все матрицы с ненулевым определителем. Если элемент x обратим, то определены степени с отрицательным показателем: 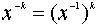. Наконец, отметим, что если x и y обратимы, то элемент 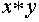также обратим и 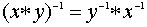. (Сначала мы одеваем рубашку, а потом куртку; раздеваемся же в обратном порядке!).

Определение (абстрактной) группы.

Пусть на множестве G определена алгебраическая операция (*). (G ,*) называется группой, если

Операция (*) ассоциативна на G. Для этой операции существует нейтральный элемент e (единица группы). Каждый элемент из G обратим.

Примеры групп.

Любая группа преобразований. (Z, +), (R, +), (C, +).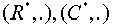 Матричные группы: 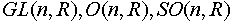- невырожденные квадратные матрицы порядка n, ортогональные матрицы того же порядка, ортогональные матрицы с определителем 1. 3. Простейшие свойства групп. В любой группе выполняется закон сокращения: 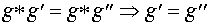(левый закон сокращения; аналогично, имеет место и правый закон). Доказательство. Домножим равенство слева на 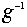и воспользуемся свойством ассоциативности: 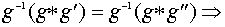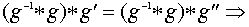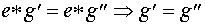. Признак нейтрального элемента: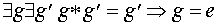

Доказательство Применим к равенству 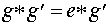закон сокращения.

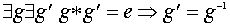Признак обратного элемента: Доказательство Применим закон сокращения к равенству 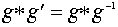. Единственность обратного элемента. Обратный элемент определен однозначно. Следует из п.3. Существование обратной операции. Для любых двух элементов 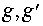произвольной группы G уравнение 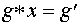имеет и притом единственное решение. Доказательство Непосредственно проверяется, что 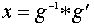(левое частное элементов 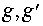) является решением указанного уравнения. Единственность вытекает из закона сокращения, примененного к равенству 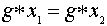. Аналогично устанавливается существование и единственность правого частного. 4. Изоморфизм групп.

Определение.

Отображение 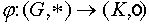двух групп G и K называется изоморфизмом , если

1.Отображение j взаимно однозначно. 2.Отображение j сохраняет операцию: .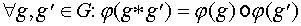

Поскольку отображение обратное к j также является изоморфизмом, введенное понятие симметрично относительно групп G и K , которые называются изоморфными.

Примеры.

1.Группы поворотов плоскост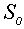и и 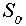вокруг точек 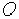и 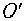изоморфны между собой. Аналогично, изоморфными будут и группы, состоящие из поворотов пространства относительно любых двух осей.

2.Группа диэдра 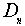и соответствующая пространственная группа 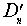изоморфны.

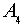Группа тетраэдра T изоморфна группе состоящей из четных подстановок четвертой степени. Для построения изоморфизма достаточно занумеровать вершины тетраэдра цифрами 1,2,3,4 и заметить, что каждый поворот, совмещающий тетраэдр с собой некоторым образом переставляет его вершины и, следовательно, задает некоторую подстановку множества{1,2, 3, 4} Повороты вокруг оси, проходящей через некоторую вершину (например 1), оставляет символ 1 на месте и циклически переставляет символы 1, 2, 3. Все такие перестановки - четные. Поворот вокруг оси, соединяющей середины ребер (например, 12 и 34 ) переставляет символы 1 и 2 , а также 3 и 4. Такие перестановки также являются четными. Формула 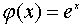определяет взаимно однозначное соответствие между множеством R вещественных чисел и множеством 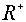положительных чисел. При этом 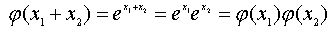. Это означает, что 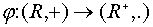является изоморфизмом.

Замечание. В абстрактной алгебре изоморфные группы принято считать одинаковыми. По существу это означает, что игнорируются индивидуальные свойства элементов группы и происхождение алгебраической операции.

5. Понятие подгруппы.

Непустое подмножество 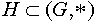называется подгруппой, если 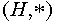само является группой. Более подробно это означает, что 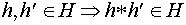, 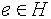и .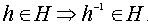

Признак подгруппы.

Непустое подмножество 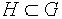будет подгруппой тогда и только тогда, когда .

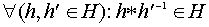Доказательство.

В одну сторону это утверждение очевидно. Пусть теперь 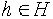- любой элемент. Возьмем 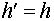в признаке подгруппы. Тогда получим 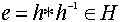. Теперь возьмем 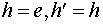. Тогда получим .

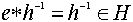Примеры подгрупп.

Рекомендуем скачать другие рефераты по теме: банк курсовых, шпори политология.





1  2  3  4  5  6 | Следующая страница реферата