Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Все эти классы состоят из 2 элементов.

Классы сопряженных элементов G относительно подгруппы H:

, , , .

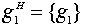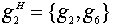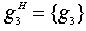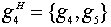В то же время,

, , .

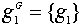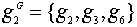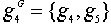Теорема Лагранжа.

Пусть H подгруппа конечной группы G. Тогда порядок H является делителем порядка G.

Доказательство.

По свойству орбит G представляется в виде объединения непересекающихся смежных классов: 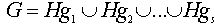. Поскольку все смежные классы состоят из одинакового числа элементов, 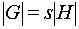, откуда и вытекает теорема.

Замечание. Число s левых (или правых) смежных классов называется индексом подгруппы .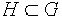

Следствие.

Две конечные подгруппы группы G порядки которых взаимно просты пересекаются только по нейтральному элементу.

В самом деле, если 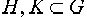эти подгруппы, то 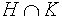их общая подгруппа и по теореме Лагранжа 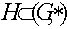- общий делитель порядков H и K то есть 1.

8. Нормальные подгруппы. Факторгруппы.

Пусть 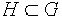любая подгруппа и 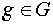-любой элемент. Тогда 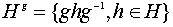также является подгруппой G притом изоморфной H, поскольку отображение сопряжения 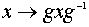является изоморфизмом. Подгруппа 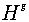называется сопряженной по отношению к подгруппе H.

Определение.

Подгруппа H называется инвариантной или нормальной в группе G, если все сопряженные подгруппы совпадают с ней самой: .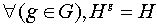

Равенство 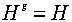можно записать в виде Hg = gH и таким образом, подгруппа инвариантна в том и только в том случае, когда левые и правые смежные классы по этой подгруппе совпадают.

Примеры.

В коммутативной группе все подгруппы нормальны, так как отображение сопряжения в такой группе тождественно. В любой группе G нормальными будут , во первых, тривиальная подгруппа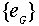 и, во вторых, вся группа G. Если других нормальных подгрупп нет, то G называется простой. В рассмотренной выше группе 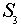подгруппа 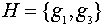не является нормальной так как левые и правые смежные классы не совпадают. Сопряженными с H будут подгруппы 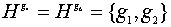и . 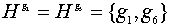Если 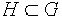- любая подгруппа, то ее централизатор Z = Z(H,G) - нормальная подгруппа в G , так как для всех ее элементов z 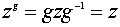. В частности, центр Z(G) любой группы G -нормальная подгруппа. Подгруппа H индекса 2 нормальна. В самом деле, имеем 2 смежных класса : H и Hg = G-H = gH.

Теорема (свойство смежных классов по нормальной подгруппе).

Если подгруппа H нормальна в G, то множество всевозможных произведений элементов из двух каких либо смежных классов по этой подгруппе снова будет одним из смежных классов, то есть .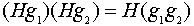

Доказательство.

Очевидно, что для любой подгруппы H HH=H.Но тогда

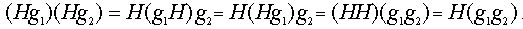
Таким образом, в случае нормальной подгруппы H определена алгебраическая операция на множестве смежных классов. Эта операция ассоциативна поскольку происходит из ассоциативного умножения в группе G. Нейтральным элементом для этой операции является смежный класс 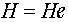. Поскольку 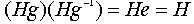, всякий смежный класс имеет обратный. Все это означает, что относительно этой операции множество всех (левых или правых) смежных классов по нормальной подгруппе является группой. Она называется факторгруппой группы G по H и обозначается G/H. Ее порядок равен индексу подгруппы H в G.

9 Гомоморфизм.

Гомоморфизм групп - это естественное обобщение понятия изоморфизма.

Рекомендуем скачать другие рефераты по теме: банк курсовых, шпори политология.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата