
Абстрактная теория групп
| Категория реферата: Рефераты по математике
| Теги реферата: доклад на тему животные, сочинения по литературе
| Добавил(а) на сайт: Rudov.
Предыдущая страница реферата | 1 2 3 4 5 6 | Следующая страница реферата
Для групп преобразований новое и старое понятие подгруппы равносильны между собой.
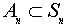 - подгруппа четных подстановок.
- подгруппа четных подстановок.
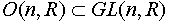
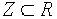 и т.д.
Пусть G - любая группа и
и т.д.
Пусть G - любая группа и 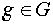 -
любой фиксированный элемент. Рассмотрим множество
-
любой фиксированный элемент. Рассмотрим множество 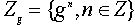 всевозможных
степеней этого элемента. Поскольку
всевозможных
степеней этого элемента. Поскольку 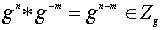 ,
рассматриваемое множество является подгруппой. Она называется циклической
подгруппой с образующим элементом g .
Пусть
,
рассматриваемое множество является подгруппой. Она называется циклической
подгруппой с образующим элементом g .
Пусть 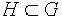 любая подгруппа Рассмотрим множество
любая подгруппа Рассмотрим множество 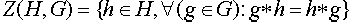 - централизатор подгруппы H в группе G. Из определения вытекает, что если
- централизатор подгруппы H в группе G. Из определения вытекает, что если 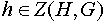 , то
, то 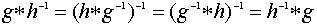 , то есть
, то есть 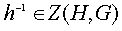 . Теперь ясно, что если
. Теперь ясно, что если 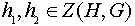 , то и
, то и 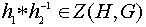 и значит централизатор является подгруппой. Если группа G коммутативна, то
и значит централизатор является подгруппой. Если группа G коммутативна, то 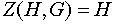 . Если G=H, то централизатор состоит из тех элементов, которые перестановочны со всеми элементами группы; в этом случае он называется центром группы G и обозначается Z(G).
. Если G=H, то централизатор состоит из тех элементов, которые перестановочны со всеми элементами группы; в этом случае он называется центром группы G и обозначается Z(G).
Замечание об аддитивной форме записи группы.
Иногда, особенно когда операция в группе коммутативна, она обозначается (+) и называется сложением. В этом случае нейтральный элемент называется нулем и удовлетворяет условию: g+0=g. Обратный элемент в этом случае называется противоположным и обозначается (-g). Степени элемента g имеют вид g+g+...+g , называются кратными элемента g и обозначаются ng.
6. Реализация абстрактной группы как группы преобразований.Существует несколько способов связать с данной абстрактной группой некоторую группу преобразований. В дальнейшем, если не оговорено противное, знак алгебраической операции в абстрактной группе будет опускаться.
Пусть 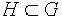 некоторая подгруппа.
некоторая подгруппа.
А) Для каждого 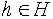 определим отображение
определим отображение 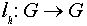 (левый сдвиг на элемент h) формулой
(левый сдвиг на элемент h) формулой 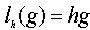 .
.
Теорема 1
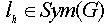 Множество L(H,G)=
Множество L(H,G)= 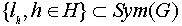 является группой преобразований множества G.
Соответствие:
является группой преобразований множества G.
Соответствие: 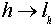 является изоморфизмом групп H и L(H,G).
является изоморфизмом групп H и L(H,G).
Доказательство.
Надо проверить, что отображение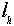 взаимно однозначно для всякого
взаимно однозначно для всякого 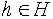 .
Если
.
Если 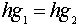 , то
, то 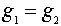 по закону сокращения. Значит
по закону сокращения. Значит 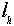 инъективно. Если
инъективно. Если 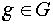 любой элемент,
то
любой элемент,
то 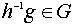 и
и 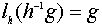 так что
так что 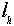 к тому же и сюръективно.
Обозначим через · операцию композиции в
группе Sym(G) взаимно однозначных отображений
к тому же и сюръективно.
Обозначим через · операцию композиции в
группе Sym(G) взаимно однозначных отображений 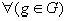 .
Надо проверить, что
.
Надо проверить, что 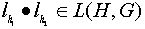 и
и 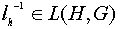 .
Пусть
.
Пусть 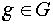 любой элемент. Имеем:
любой элемент. Имеем: 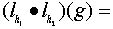
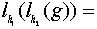
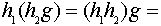
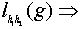
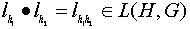 ;
;
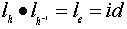 и значит,
и значит, 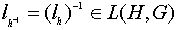 .
Пусть
.
Пусть 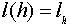 . Надо проверить, что
l взаимно однозначно и сохраняет операцию. По построению l сюръективно. Инъективность
вытекает из закона правого сокращения:
. Надо проверить, что
l взаимно однозначно и сохраняет операцию. По построению l сюръективно. Инъективность
вытекает из закона правого сокращения: 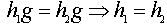 .
Сохранение операции фактически уже было установлено выше:
.
Сохранение операции фактически уже было установлено выше: 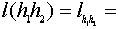
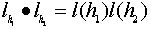 .
.
Следствие.
Любая абстрактная группа изоморфна группе преобразований некоторого множества (Достаточно взять G=H и рассмотреть левые сдвиги).
Для случая конечных групп получается теорема Кэли:
Любая группа из n элементов изоморфна подгруппе группы 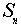 подстановок степени n.
подстановок степени n.
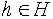 определим отображение
определим отображение 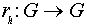 (правый сдвиг на элемент h) формулой
(правый сдвиг на элемент h) формулой 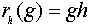 .
.
Теорема B.
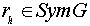 .
Множество
.
Множество 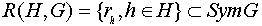 является группой
преобразований множества G.
Соответствие
является группой
преобразований множества G.
Соответствие 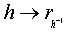 является изоморфизмом
групп H и R(H,G).
является изоморфизмом
групп H и R(H,G).
Доказательство теоремы B вполне аналогично доказательству теоремы A. Отметим только, что 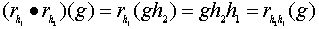 . Именно поэтому в пункте 3 теоремы В появляется не
. Именно поэтому в пункте 3 теоремы В появляется не 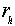 , а
, а 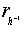 .
.
С) Для каждого 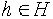 определим
определим 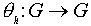 (сопряжение или трансформация элементом h ) формулой
(сопряжение или трансформация элементом h ) формулой 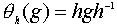 .
.
Теорема С.
Каждое отображение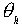 является изоморфизмом группы G с собой (автоморфизмом группы G).
Множество
является изоморфизмом группы G с собой (автоморфизмом группы G).
Множество 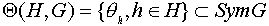 является группой преобразований множества G.
Отображение
является группой преобразований множества G.
Отображение 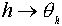 сюръективно и сохраняет операцию.
сюръективно и сохраняет операцию.
Доказательство.
Поскольку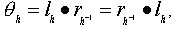 , отображение
, отображение 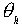 взаимно однозначно как композиция двух отображений такого типа. Имеем:
взаимно однозначно как композиция двух отображений такого типа. Имеем: 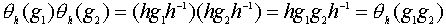 и потому
и потому 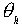 сохраняет операцию.
Надо проверить, что
сохраняет операцию.
Надо проверить, что 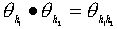 и
и 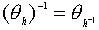 . Оба равенства проверяются без труда.
Сюръективность отображения
. Оба равенства проверяются без труда.
Сюръективность отображения 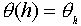 имеет место по определению. Сохранение операции уже было проверено в пункте 2.
имеет место по определению. Сохранение операции уже было проверено в пункте 2.
Замечание об инъективности отображения q .
В общем случае отображение q
не является инъективным. Например, если группа H коммутативна, все преобразования 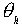 будут тождественными и группа
будут тождественными и группа 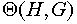 тривиальна. Равенство
тривиальна. Равенство 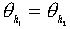 означает, что
означает, что 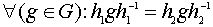 или
или 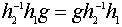 (1) В связи с этим удобно ввести следующее определение: множество
(1) В связи с этим удобно ввести следующее определение: множество 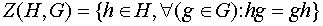 называется централизатором подгруппы
называется централизатором подгруппы 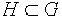 . Легко проверить, что централизатор является подгруппой H. Равенство (1) означает, что
. Легко проверить, что централизатор является подгруппой H. Равенство (1) означает, что 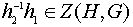 . Отсюда вытекает, что если централизатор подгруппы H в G тривиален, отображение q
является изоморфизмом.
. Отсюда вытекает, что если централизатор подгруппы H в G тривиален, отображение q
является изоморфизмом.
Пусть, как и выше, 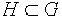 некоторая подгруппа. Реализуем H как группу L(H,G) левых сдвигов на группе G. Орбита
некоторая подгруппа. Реализуем H как группу L(H,G) левых сдвигов на группе G. Орбита 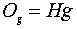 называется левым смежным классом группы G по подгруппе H. Аналогично, рассматривая правые сдвиги, приходим к правым смежным классам
называется левым смежным классом группы G по подгруппе H. Аналогично, рассматривая правые сдвиги, приходим к правым смежным классам 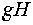 .Заметим, что
.Заметим, что 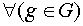 стабилизатор St(g, L(H,G)) (как и St(g, R(H,G)) ) тривиален поскольку состоит из таких элементов
стабилизатор St(g, L(H,G)) (как и St(g, R(H,G)) ) тривиален поскольку состоит из таких элементов 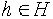 , что hg=g
, что hg=g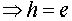 . Поэтому, если группа H конечна, то все левые и все правые смежные классы состоят из одинакового числа элементов, равного
. Поэтому, если группа H конечна, то все левые и все правые смежные классы состоят из одинакового числа элементов, равного 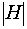 .
.
Орбиты группы 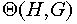 называются классами сопряженных элементов группы G относительно подгруппы H и обозначаются
называются классами сопряженных элементов группы G относительно подгруппы H и обозначаются 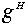 Если G=H, говорят просто о классах сопряженных элементов группы G. Классы сопряженных элементов могут состоять из разного числа элементов . Это число равно
Если G=H, говорят просто о классах сопряженных элементов группы G. Классы сопряженных элементов могут состоять из разного числа элементов . Это число равно 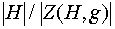 , где Z(H,g) подгруппа H , состоящая из всех элементов h перестановочных с g.
, где Z(H,g) подгруппа H , состоящая из всех элементов h перестановочных с g.
Пример.
Пусть 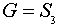 - группа подстановок степени 3. Занумеруем ее элементы:
- группа подстановок степени 3. Занумеруем ее элементы: 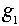 =(1,2,3);
=(1,2,3); 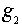 =(1,3,2);
=(1,3,2); 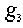 =(2,1,3);
=(2,1,3); 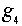 =(2,3,1);
=(2,3,1); 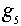 =(3,1,2);
=(3,1,2); 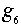 =(3,2,1). Пусть
=(3,2,1). Пусть 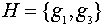 . Легко проверить, что левые смежные классы суть:
. Легко проверить, что левые смежные классы суть:
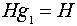 ,
, 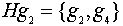 ,
, 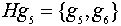 .
.
Правые смежные классы:
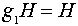 ,
, 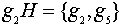 ,
, 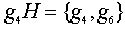 .
.
Рекомендуем скачать другие рефераты по теме: банк курсовых, шпори политология.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 | Следующая страница реферата
 Главная
Главная