Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

5 = 5(И) 3 = |9 – 15 + 9|

3 = 3(И)

Ответ: x1=1; x2=3

4.2.Использование геометрической интерпритации модуля для решения уравнений.

Геометрический смысл модуля разности величин-это расстояние между ними. Например, геометрический смысл выражения |x – a | -длина отрезка координатной оси, соединяющей точки с абсцисами а и х . Перевод алгеб-раической задачи на геометрический язык часто позволяет избежать громоздких решений.

Пример7. Решим уравнение |x – 1| + |x – 2|=1 с использованием геометрической интерпритации модуля.

Будем рассуждать следующим образом: исходя из геометрической интерпри-тации модуля, левая часть уравнения представляет собой сумму расстояний от некторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок [1; 2].

Ответ: х  [1; 2]

Пример8. Решим уравнение |x – 1| - |x – 2|=1 1 с использованием геометрической интерпритации модуля.

Будем рассуждать аналогично предыдущему примеру, при этом получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Следовательно решением данного уравнения будет являтся не отрезок, заключенный между точками 1 и 2, а луч, выходящий из точки 2, и направленный в положительном направлении оси ОХ.

Ответ: х [2; +)

Обобщением вышеприведенных уравнений являются следующие равносильные переходы:

|x – a| + |x – b|=b – a, где b  a  a  x  b

|x – a| - |x – b|=b – a, где b  a  x  b

4.3. Графики простейших функций, содержащих знак абсолютной величины

Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): "Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна -- произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя -- с абсциссой, большей большего из корней.

Например:

1)f(x)=|x - 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1)

2) f(x)=|x - 1| + |x – 2| Вычисляя значение функиции в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из двух отрезков прямых.(рис.2)

3) f(x)=|x - 1| + |x – 2| + |x – 3| Для построения графика вычислим значения функции в точках 1, 2, 3, 0 и 4 (рис.3)

4) f(x)=|x - 1| - |x – 2| График разности строится аналогично графику суммы, тоесть по точкам 1, 2, 0 и 3.

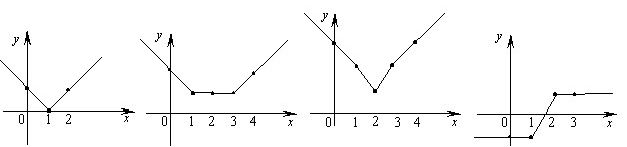
рис1. рис2. рис3. рис4.

4.4.Решение нестандартных уравнений, содержащих модули.

Пример9. Решить уравнение 3| x + 2 | + x2 + 6x + 2 = 0.

Решение.

Рассмотрим два случая.

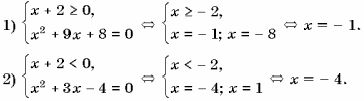
Рекомендуем скачать другие рефераты по теме: изложение русский язык 6 класс, личные сообщения.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата