Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Д – алгебра диагональных операторов в Н. Пусть μ1 – мера на Т, эквивалентная μ,

Н1 =Н(t) dμ1(t) , π1 =π(t) dμ1(t),

Д1 – алгебра диагональных операторов в Н1. Тогда канонический изоморфизм преобразует π в π1 и Д в Д1.

Доказательство. Пусть ρ(t)=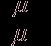. Канонический изоморфизм из Н в Н1 есть изометрический изоморфизм, который переводит х =x(t) dμ(t)Н в

Ux = ρ-1/2х(t) dμ1(t).

Пусть α А. Имеем

π1(α)Ux = π(t)(α) ρ-1/2 х(t) dμ1(t) = Uπ(t)(α) х(t) dμ(t) = Uπ(α)x,

поэтому и преобразуем π в π1. Тогда если SД, то аналогично SUx = USx, для любого хН.

Определение 2.14. Пусть Т, Т1 – борелевские пространства; μ, μ1 – меры на Т и Т1 соответственно; ε = ((H(t))tT, Г), Z1 = ((H1(t1))t1T1, Г), - μ-измеримое и μ1-измеримое поля гильбертовых пространств. Пусть η: Т→Т1 – борелевский изоморфизм, переводящий μ в μ1; η-изоморфизм ε на ε1 называется семейство (V(t))tT, обладающее следующими свойствами:

для любого tT отображение V(t) является изоморфизмом Н(t) на Н1(η(t));

для того, чтобы поле векторов t→x(t)H(t) на Т было μ-измеримо, необходимо и достаточно, чтобы поле η(t)→V(t)х(t) Н1(η(t)) на Т1 было μ1-измеримо.

Отображение, переводящее поле хН =Н(t) dμ(t) в поле η(t))→V(t)х(t) Н1 = Н1(t) dμ1(t) , есть изоморфизм Н на Н1, обозначаемый V(t) dμ(t).

Теорема 2.11. Пусть Т – борелевское пространство; μ – мера на Т, t→H(t) – μ- измеримое поле гильбертовых пространств на Т, t→ π(t) - μ- измеримое поле представлений А в H(t),

Н =Н(t) dμ(t), π ==π(t) dμ(t),

Д – алгебра диагональных операторов в Н. Определим аналогичным образом Т1, μ1, t1→H1(t1), t1→ π1(t1), Н1, π1, Д1.

Предположим, что существует:

N, N1 – борелевские подмножества Т и Т1, такие что μ (N) = μ (N1) = 0;

борелевский изоморфизм η: TN →TN1, преобразует μ в μ1;

η-изоморфизм t→V(t) поля t→Н(t) (tZN) на поле t1→Н1(t1) (t1Т1N1) такой, что V(t) преобразует π(t) в π1(η(t)) для каждого t.

Тогда V =V(t)dμ(t) преобразует Д в Д1 и π в π1.

Доказательство. Обозначим через It, It1 единичные операторы в Н(t) и Н1(t1). Если fL∞(T, μ) и если f1 – функция на Т1N1, получаемая из f|(TN) при помощи η, то V преобразует f(t)It dμ(t) в f1(t1) It1 dμ1(t1), поэтому V преоб- разует Д в Д1. С другой стороны, пусть αА и х = х(t) dμ(t)Н.

Тогда

Vπ(α)х = Vπ(t)(α) х(t) dμ(t) = V(η-1(t1)) π(η-1(t1))(α) х(η-1(t1)) dμ1(t1) = π1(t1)(α) V(η-1(t1)) х(η-1(t1)) dμ1(t1) = π1 (α) V х

Поэтому V преобразует π в π1.

Приведем примеры прямых интегралов.

Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.





Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата