Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

Множество максимальных векторов всюду плотно в Н. Пусть существует счетное разложение Н = Нηк. Пусть {ζi} – последовательность, в которой каждый из векторов ηi встречается бесконечное число раз. Определим ξк индуктивно, так, чтобы выполнялись условия:

ξк+1 – максимальный вектор в (Нξi)┴,

d (ζк, Нξi) ≤ .

Тогда разложение Н = Нξк такое что ξк>ξк+1 и μк>μк+1 .

Пусть представления πμ в L2(Т, μ) и πν в L2(Т, ν) эквивалентны. Пусть v:L2(Т, μ) →L2(Т, ν) устанавливающий их эквивалентность изоморфизм. Положим f=1, а=v(f), тогда для любой непрерывной функции g на Т v(g)=vπμ(g)f = πν (g)vf = πν (g)a = ga. Так как v – изометрическое отображение, то dμ=|a|2dν. Таким образом мера μ абсолютно непрерывна по мере ν. Аналогично, рассматривая обратный оператор, получаем, что ν абсолютно непрерывна по μ, то есть эти меры эквивалентны. Значит существует разложение Н΄ = (С2L2(Т, μк)), где μ1>μ2>… и соответствующие этим мерам представления неприводимы и неэквивалентны. Это доказывает равенство (2.4.). Тогда из (2.4.) следуют формулы:

P1 = P1,0 P1,1  ((Iк ))

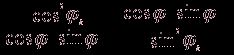
Р2 = P0,1 P1,1 (Iк ))

Iк – единичный оператор в L2((0, ), dρк).

Теорема 2.4. (спектральная теорема в форме разложения единицы). Паре ортопроекторов Р1 и Р2 в сепарабельном гильбертовом пространстве Н соответствует разложение

Н = Н0,0Н0,1Н1,0 Н1,1 С2Н(φ)dЕ(φ) (2.7.)

в прямой интеграл инвариантных относительно Р1, Р2 подпространств и определенное на Т = (0, ) разложение dЕ(φ) единичного оператора I+=E(0, ) в Н+ =С2Н(φ)dЕ(φ), такое что имеет место равенство

P1 = P1,0 P1,1  I+ (2.8.)

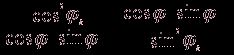
Р2 = P0,1 P1,1 dЕ(φ) (2.9.)

Доказательство. Всякий самосопряженный оператор А, действующий в Н, изометрически изоморфен оператору умножения на независимую переменную в пространстве L2(R, dρк), где ρк зависит от разложения единицы оператора А. Тогда доказательство спектральной теоремы в форме разложения единицы следует непосредственно из спектральной теоремы в форме операторов умножения.

Глава III. Спектр суммы двух ортопроекторов

§1. Спектр суммы двух ортопроекторов в унитарном пространстве

1.1. Спектр ортопроектора в гильбертовом пространстве.

Теорема 1.1. Пусть Н – гильбертово пространство. Если Р – ортопроектор, то (Р) = р (Р) = {0, 1}, где р (Р) – точечный спектр при условии, что Р ≠ 0 и Р ≠ I.

Доказательство. Рассмотрим выражение Рх - λх = y, х, y Н, λ С. Тогда (1 - λ) Рх = Рy . Если λ ≠ 1, то Рх = Рy. Если х ≠ 1, то х = (Рy - y), тогда (Р) = {0, 1}.

Так как Р ≠ 0 и Р ≠ I, то существует х ≠ 0 такой, что Рх ≠ 0. Тогда Р(Рх) = Рх, то есть 1р (Р). Существует y ≠ 0: (I - Р)y ≠ 0, тогда Р(I - Р)y = 0 = 0 · (I - Р)y, то есть 0 р (Р). Итак, (Р) = р (Р) = {0, 1}.

1.2. Постановка задачи. Пусть заданы два ортопроектора Р1 и Р2 в унитарном пространстве Н. Тогда мы знаем спектр каждого из них. Найдем спектр суммы Р1 + Р2 в неприводимых представлениях.

1.3. Спектр в одномерном пространстве. Пусть dimH =1. Пусть, как и выше, Нк – область значений оператора Рк к = 1,2. Обозначим через А = Р1 + Р2 и найдем (А).

1) Р1 = Р2 = 0, то для любого х Н Ах = 0 или Ах = 0 · х, то есть 0  (А).

2) Р1 = 0, Р2 = I, то для любого х Н2 = Н Ах = х, то есть 1  (А).

3) Р1 = I, Р2 = 0, то для любого х Н1 = Н Ах = х.

Рекомендуем скачать другие рефераты по теме: решебник 6, евгений сочинение.





Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата