Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Итак, под корнями стоят положительные числа, следовательно, уравнение эллипса.

2. I3>0 в данном случае под корнем стоят отрицательные числа, следовательно уравнение не определяет действительного геометрического образа.

3. I3=0 в данном случае т(0,0) – случай вырождения эллипса.

ТЕОРЕМА О ЛИНИЯХ ГИПЕРБОЛИЧЕСКОГО ТИПА.

Теорема: Пусть уравнение (1) определяет линию гиперболического типа. Т.е. I2<0, I3¹ 0 - ур-е (1) определяет гиперболу; I3=0 – пару пересекающихся прямых.

Доказательство: I2<0; I2= a11’’a22’’ < 0. Пусть a11’’>0; a22’’<0

Пусть I3>0

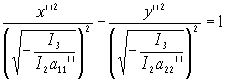
В данном случае мы имеем гиперболу с действительной осью ОХ.

Пусть I3<0

-(-а11’’)x’’2+a22’’ y’’2= -I3/I2

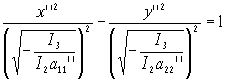
В этом случае мы имеем гиперболу с действительной осью ОY

Пусть I3=0

а11’’x’’2-(-a22’’)y’’2=0

АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ КРИВЫХ 2-ГО ПОРЯДКА.

Пусть крива второго порядка задана уравнением (1). Рассмотрим квадратную часть этого уравнения: u(x,y)= a11x2+2a12xy+a22y2

Определение: ненулевой вектор (a , b ) координаты которого обращают в ноль квадратичную часть называется вектором асимптотического направления заданной кривой.

(a , b ) – вектор асимптотического направления.

a11a 2+2a12a b +a22b 2=0 (*)

Рассмотрим (a ’, b ’) параллельный (a , b ): следовательно . Дробь a /b характеризует вектор асимптотического направления.

Рекомендуем скачать другие рефераты по теме: конспект, оформление доклада титульный лист.





Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата