Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

В приложении к другой работе о рядах (1694 г.) Я. Бернулли сформулировал несколько тезисов.

1. Существуют спирали, которые совершают бесконечное число витков вокруг полюса, но имеют конечную длину.

2. Существуют кривые, которые, подобно эллипсу, замкнуты и, подобно параболе, уходят в бесконечность, например ay2=х2(b+х).

3. Существуют кривые, состоящие из двух ветвей, например ау2=х{а2—х2),

4. Существуют неограниченные поверхности с конечной площадью.

5. Существуют неограниченные поверхности с бесконечной площадью, но такие, что соответствующие им тела вращения обладают конечным объемом.

   Я. Бернулли увлекался также и изопериметрическими задачами. Древнейшая из них—задача легендарной основательницы Карфагена и его первой царицы Дидоны. Легенда такова. Дидона бежала от отца, тирского царя, и достигла Африки, где купила у туземцев участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Она разрезала шкуру на узкие полоски и связала из них длинную ленту. Спрашивается, какой формы должна быть фигура, оцепленная лентой данной длины, чтобы площадь фигуры была наибольшей?

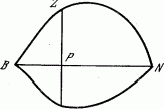   Ван-дер-Варден пишет, что Зенодор, живший вскоре после Архимеда, высказал 14 предложений относительно изопериметрических фигур. Он утверждал, что из всех фигур (кругов и многоугольников), имеющих одинаковый периметр, круг будет наибольшим, а также и то, что из всех пространственных тел с одинаковой поверхностью наибольшим будет шар.

Решение задачи содержится в записных книжках Я. Бернулли и помещено в майском номере «Acta  Eruditorum»   за 1701 г. Я. Бернулли и здесь применил высказанный ранее принцип: поскольку площадь должна быть экстремальной, этим же свойством должна обладать и любая ее элементарная часть. Он получил дифференциальное уравнение третьего порядка и впоследствии проинтегрировал его.

К. А. Рыбников пишет: «Таким образом, решение изопериметрической задачи означало очень важный, принципиально новый этап в истории вариационного исчисления; оно дало возможность решать более сложные вариационные задачи, им был сделан важный шаг на пути решения вариационных задач».        

При изучении свойств сочетаний и фигурных чисел Я. Бернулли встретился с суммированием степеней натуральных чисел Sm = å km

Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, ука зал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы сумм от S(п) до S(п10):

   S (n) = n2/2 +n/2

   S (n2) = n3/3 + n2/2+ n/6

   S (n3) = n4/4 + n3/2 + n2/4

   S (n4) = n5/5 + n4/2 + n3/3 – n/30

   S (n5) = n6/6 + n5/2 + 5n4/12 - n2/12

   S (n6) = n7/7 + n6/2 + n5/2 - n3/6 + n/42

   S (n7) = n8/8 + n7/2 + 7n6/12 - 7n4/24 + n2/12

   S (n8) = n9/9 + n8/2 + 2n7/3 - 7n5/15 + 2n3/9 – n/30

   S (n9) = n10/10 + n9/2 + 3n8/4 - 7n6/10 + n4/2 - n2/12

   S (n10) = n11/11 + n10/2 + 5n9/9 – n7 + n5 - n3/2 + 5n/66

        Затем Я. Бернулли указал общую формулу

S(nc) = nc+1/c+1 + 1/2*nc + 1/2*(  )Anc-1 + 1/4*(  )Bnc-3 + 1/6*(  )Cnc-5 + 1/8*(  )Dnc-7+ …

Здесь (  ), (  ) … - числа сочетаний; показатели степени n убывают, последний член в правой части содержит n или n2. Числа A, B, C, D … - коэффициенты при n в выражениях S(n2), S(n4), S(n6), … Именно: А=1/6, В=-1/30, С=1/42, D=-1/30, …Бернулли формулирует общее правило для вычисления этих чисел: сумма коэффициентов в выражениях S(n), S(n2), S(n3), … равна единице. Например, 1/9+1/2+2/3-7/15+2/9+D=1. Отсюда D=-1/30.

Рекомендуем скачать другие рефераты по теме: жизнь реферат, реферат по физкультуре.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата