Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Замечание: Пусть теперь область Д ограничена следующими линиями:

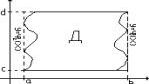
x=y1(y) c £ y £ d – слева; x=y2(y) c £ y £ d – справа;

x = c – сверху; x = d – снизу.  И пусть

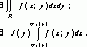
Тогда аналогично предыдущему можно показать, что существует повторный интеграл и

Если же функция f(x;y) такова, что существует двойной интеграл, существует оба повторных, то одновременно имеют место формулы (1) и (2) и можно пользоваться любой из них.Вопрос №5 

Формула Грина.

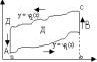
Теорема: Пусть задана область Д огран. след. кривыми:

y=j1(x)    a £ x £ b

y=j2(x)    a £ x £ b

x=a   ,   x=b, где ф-ции j1 и j2 непрер. на (a,b). Пусть в этой области задаётся функция P(x,y) – непрер. и имеющая непрер. частную производную: , тогда имеет место след. равенство:

Доказательство:

Рассмотрим двойной интеграл, стоящий справа в формуле(1). Т.к. под интегралом стоит непрер. функция, то такой двойной интеграл существует, также существует одномерный интеграл и его можно вычислить через повторный:

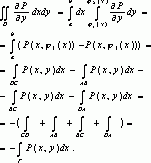
 Теорема: Пусть задана область Д огран.:

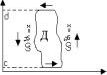
y=j1(x)    с £ x £ d

y=j2(x)    c £ x £ d

x=c   ,   x=d. И пусть в этой области задаётся функция Q(x,y) – непрер. и имеющая непрер. частную производную: , тогда имеет место след. равенство:

Cкладываем формулы (1) и (2) и получаем следующую формулу Грина для области Д:

Рекомендуем скачать другие рефераты по теме: шпаргалки для студентов, титульный дипломной работы.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата