Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата



Пересечение прямой и плоскости если прямые || пл., то множество пересечений – единственная точка; если прямые II пл., то M ¹ Æ ; если прямые совпадают, то множество пересечений = множество прямой.

Пересечение системы множеств:

Разностью 2-х множеств А и В называется множество, состоящее из всех элементов А, не входящих в В.

С = А В

A = {a,b,d}; B = {b,c,d,h} C = A B={a}.

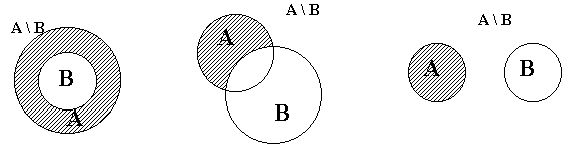
В отличии от предыдущих операций разность: 1) строго двухместна;

2) не коммутативна, т.е. AB ¹ BA.

4) дополнение

E – универсальное множество.

-- дополнение

Операции объединения, пересечения и дополнения называются Булевыми.

Основные законы операций над множествами.

Некоторые свойства È , Ç похожи на алгебраические операции, однако многие свойства операций над множествами все же отличаются.

Основные свойства AUB=BUA; AÇ B=BÇ A – переместительный закон объединения и пересечения. (АUB)UC = AU(BUC); (AÇ B)Ç C=AÇ (BÇ C) – сочетательный закон. АUÆ =A, AÇ Æ =Æ , A Æ =A, A A=Æ

1,2,3 – есть аналог в алгебре.

3.а) Æ A = Æ - нет аналога.

Æ ; E A =; A E=Æ ; AUA=A; AÇ A=A; AUE=E; AÇ E=A;

5.а) свойства 1-4 очевидны и не нуждаются в доказательствах.

AÇ (BUC)=(AÇ B)(AÇ C) – есть аналогичный распределительный закон Ç относительно U. Прямые произведения и функции

Прямым декартовым “х” множеством А и В называется множество всех пар (a;b), таких, что аÎ А, bÎ B.

С=AхВ, если А=В то С=А2.

Прямыми “х” n множеств A1x,…,xAn называется множество векторов (a1,…an) таких, что a1Î A1,…, AnÎ An.

Через теорию множеств введем понятие функции.

Подмножество FÎ Mx x My называется функцией, если для каждого элемента хÎ Mx найдется yÎ Му не более одного.

(x;y)Î F, y=F(x).

Соответствие между аргументом и функцией можно изобразить с помощью диаграммы Венна:

Определение: Между множествами MX и MY установлено взаимноодназночное соответствие, если каждому хÎ MX соответствует 1 элемент yÎ MY и обратное справедливо.

Пример: 1) (х,у) в круге

x=2 à y=2

y=2 à x=2..4

не взаимнооднозначное соответствие.

Рекомендуем скачать другие рефераты по теме: контрольная работа 10 класс, контрольная работа 8.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата